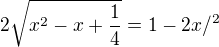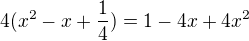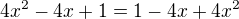Matematické Fórum

Hanuna2 · 03. 03. 2017 14:25

Dobry den,

mam rovnici:
$2 \sqrt{x^{2}-x+\frac{1}{4}} =1-2x$
po upravach mi vyjde 0 = 0

Df.: $\sqrt{x^{2}-x+\frac{1}{4}} \ge 0 \wedge 1-2x\ge 0$
prvni cast vyjde: 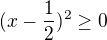$(x-\frac{1}{2})^{2}\ge 0$ , coz je splneno pro vsechna cisla, resenim je teda R
druha cast vyjde: 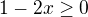$1-2x\ge 0$ , $x\le \frac{1}{2}$

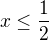
tzn. Df = (-∞, 1/2>

A co je tedy resenim?

H

misaH · 03. 03. 2017 14:29 — Editoval misaH (03. 03. 2017 14:30)

↑ Hanuna2:

No:

0=0 by znamenalo, že riešením sú všetky ( reálne) čísla.

Sú riešením všetky?

Cheop · 03. 03. 2017 14:45 — Editoval Cheop (03. 03. 2017 14:56)

↑ Hanuna2:
Po úpravách vychází toto: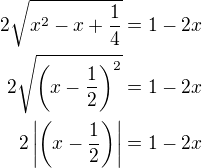
$2\sqrt{x^{2}-x+\frac{1}{4}} =1-2x\\2\sqrt{\left(x-\frac 12\right)^2}=1-2x\\2\left|\left(x-\frac 12\right)\right|=1-2x$

Opraveno dle ↑ misaH:

misaH · 03. 03. 2017 14:47 — Editoval misaH (03. 03. 2017 14:49)

↑ Cheop:

Nechýba ti tam absolútna hodnota?

Hanuna2 · 03. 03. 2017 15:05

Me upravy:

$2\sqrt{x^{2}-x+\frac{1}{4}}=1-2x /^{2}$
$4(x^{2}-x+\frac{1}{4})=1-4x+4x^{2}$
$4x^{2}-4x+1=1-4x+4x^{2}$
0=0

H

misaH · 03. 03. 2017 15:20

↑ Hanuna2:

Dobre.

A máš ešte nejaké otázky?

Hanuna2 · 03. 03. 2017 15:29

No, jake je resi rovnice, kdyz mam vysledek 0=0 a definicni obor Df = (-∞, 1/2>. Resenim je tedy K=(-∞, 1/2>?
H

misaH · 03. 03. 2017 18:13

↑ Hanuna2:

Vieš, mne sa to počítať nechce.

Ak je správne ten D(f), tak samozrejme, že zo všetkých reálnych x vyhovujú iba tie, čo tam patria.

Al1 · 03. 03. 2017 19:18

↑ Hanuna2:

Zdravím,

při stanovování definičního oboru rovnice si provedla chybnou úvahu. Sudá odmocnina, pokud je definována, je vždy číslo nezáporné. Takže tvůj požadavek 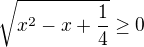$\sqrt{x^{2}-x+\frac{1}{4}} \ge 0$ je zbytečný. Co ale musí platit je $x^{2}-x+\frac{1}{4} \ge 0 \wedge 1-2x\ge 0$ .
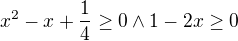Jinak je nakonec def. obor stanoven správně jako i závěr celého řešení.

Hanuna2 · 04. 03. 2017 08:49

Dekuji moc za rozbor.
H

Matematické Fórum

#1 03. 03. 2017 14:25

Rovnice s neznamou pod odmocninou

#2 03. 03. 2017 14:29 — Editoval misaH (03. 03. 2017 14:30)

Re: Rovnice s neznamou pod odmocninou

#3 03. 03. 2017 14:45 — Editoval Cheop (03. 03. 2017 14:56)

Re: Rovnice s neznamou pod odmocninou

#4 03. 03. 2017 14:47 — Editoval misaH (03. 03. 2017 14:49)

Re: Rovnice s neznamou pod odmocninou

#5 03. 03. 2017 15:05

Re: Rovnice s neznamou pod odmocninou

#6 03. 03. 2017 15:20

Re: Rovnice s neznamou pod odmocninou

#7 03. 03. 2017 15:29

Re: Rovnice s neznamou pod odmocninou

#8 03. 03. 2017 18:13

Re: Rovnice s neznamou pod odmocninou

#9 03. 03. 2017 19:18

Re: Rovnice s neznamou pod odmocninou

#10 04. 03. 2017 08:49

Re: Rovnice s neznamou pod odmocninou

Zápatí