Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 07. 03. 2017 12:16
Re: Visení vrtulníku
Dá, za předpokladu, že známe parametry vrtule.
Např. malá vrtule bude menší objem vzduchu urychlovat na větší rychlost a vyjde větší výkon. Velká bude urychlovat velké množství vzduchu o menší rychlost, takže výkon vyjde malý.
Je to dáno tím, že energie (a z ní plynoucí příkon) závisí na druhé mocnině rychlosti, kdežto hybnost (a zní plynoucí síla) závisí na první mocnině rychlosti vzduchu.
Tohle jsou základní, čistě teoretická východiska, pak přijdou na řadu další, aerodynamické parametry vrtule a pak i kabiny pod ní.
Offline
#3 08. 03. 2017 07:33
Re: Visení vrtulníku
Díky za odpověď.
Myslel jsem spíš výpočet pro obecné těleso.
Jedna moje úvaha byla tato:
Necháme těleso jednu vteřinu padat volným pádem. Pak ho náhle zastavíme. K tomuto zastavení budeme potřebovat určitou energii.
Během druhé vteřiny těleso zvedneme do původní výšky. K tomu potřebujeme další energii.
Když součet těchto energií vydělíme dvěma (tj. časem), vyjde nám průměrný výkon.
Tento děj se bude stále opakovat.
Ale něco je špatně!
Pokud zvolím čas volného pádu 10x menší (sloupec D v tabulce), vyjde mi i výkon 10x menší.
Tabulka
Offline
#4 08. 03. 2017 10:52 — Editoval LukasM (08. 03. 2017 10:55)
Re: Visení vrtulníku
↑ Pega:
Na tom nic špatně není. Akorát jsi zanedbal to, na co je ten výkon potřeba. V mezním případě, kdy těleso nestačí spadnout vůbec, ti totiž zůstane prostě visící těleso, které se nepohybuje - a tedy se na něm nekoná žádná práce. A výkon tedy bude nulový. Na to nepotřebuješ Excel.
Pokud chceš alespoň nějaký odhad výkonu (a je podle mně otázka, kolik toho bude mít společného s realitou), musí se tam někde objevit to podstatné, tedy vzduch, který je urychlovaný opačným směrem. Na těleso působí tíhová síla směrem dolů, těleso musí vzduchu předávat odpovídající hybnost, aby reakční síla (kterou působí vzduch na těleso) tuhle tíhu vyrušila. Dolů proudící vzduch má pak nějakou kinetickou energii, kterou předtím neměl - a na to je právě potřeba ten výkon.
Pravděpodobně se ale nikam nedopočítáš, ve výsledku asi zůstanou nějaké těžko určitelné parametry.
Offline
#5 08. 03. 2017 11:01
Re: Visení vrtulníku
njn, to je zcela chybná úvaha.. Už jenom to, čím by mělo být dáno, že na zabrždění je potřeba stejná E, jako Ek vzniká pádem.. Třeba padák žádnej výkon nepotřebuje a brzdí taky.
Ve skutečnosti máme vrtuli (přesněji soustavu dvou vrtulí, ale to můžeme pro začátek zanedbat), která v prvním přiblížení urychluje nějaké množství vzduchu a tím vytváří sílu.
Pod ní pak visí to obecné těleso, které má nějakou hmotnost. Z parametrů vrtule pak vyjde, kolik W/kg potřebuješ.
Ono těleso do toho taky více či méně zasahuje. Nevhodný tvar může výkon zvýšit, vhodný může být +/- neutrální, nebo můžeme vyloženě způsobit, že se s jeho pomocí rychlý proud malého průměru zvětší a zpomalí, čímž se potřebný výkon ještě sníží (tím jsme se dostali od vrtulníku až ke koandacraftu).
Prvotní úvaha tedy je, že máme proud vzduchu, jehož urychlováním získáme sílu F, která roste s rychlostí vzduchu v při potřebě výkonu P, který roste s v^2. Z toho pak plyne, že čím vyšší hmotnostní tok vzduchu m urychlujeme s cílem získat stejnou F, tím stačí menší rychlost a protože P závisí na v více, bude s rychlostí klesat výkon.
Pak je jasné, že čím větší průměr rotoru, tím menší výkon potřebujeme. V reálném vrtulníku pak narazíme na to, že když bude urychlená rychlost srovnatelná s větrem, přestane být vrtulník použitelný a vlastně ještě dříve to bude hrozný monstrum.
Offline
#6 08. 03. 2017 18:59
Re: Visení vrtulníku
↑ Pega: Ahoj, prikladám niečo podobné :-)
https://www.wired.com/2012/06/how-hard- … elicopter/
https://www.wired.com/2013/06/could-the … h-a-human/
Offline
#7 09. 03. 2017 07:25 — Editoval Pega (09. 03. 2017 07:26)
Re: Visení vrtulníku
↑ LukasM:
Na tom nic špatně není. Akorát jsi zanedbal to, na co je ten výkon potřeba. V mezním případě, kdy těleso nestačí spadnout vůbec, ti totiž zůstane prostě visící těleso, které se nepohybuje - a tedy se na něm nekoná žádná práce. A výkon tedy bude nulový. Na to nepotřebuješ Excel.
-----------------------
Ale mne nezajímá práce, kterou koná těleso, ale ta kterou koná motor, který když těleso spadne o určitou výšku, ho vynese zpátky.
Zkusím to ještě jednou.
Těleso o váze 1000 kg má pod sebou upevněný ideální raketový motor s nulovou hmotností a s regulovatelným výkonem od nuly do nekonečna (prosím nepsat, že takový motor neexistuje).
1. Počáteční stav je ten, že tato soustava visí v určité výšce nad zemí.
Motor neběží, takže těleso začne padat.
2. Po uplynutí jedné vteřiny motor vygeneruje velmi krátký impuls s takovou energií, že těleso zastaví.
3. Pak motor běží jednu vteřinu s takovým výkonem, aby vynesl těleso do původní výšky.
4. Goto 1.
Potřebné energie a vzorce jsou napsány v tabulce.
Takže prosím, jak říkal Mistr Jan Hus, poučte mne z Písma kde se mýlím.
Offline
#9 09. 03. 2017 09:43
Re: Visení vrtulníku
Ahoj Zdeňku,
Chtěl bych zdůraznit, že mi vůbec nejde o nějaký vrtulník.
To slovo jsem dal do nadpisu kvůli lepší představivosti.
Asi jsem to neměl dělat, protože teď ten nešťastný vrtulník mám stále na talíři.
Původně mi šlo o toto:
Aby se těleso o váze 1000 kg udrželo v určité výšce nad zemí, je třeba aby na ně působila síla 10 000 N směrem nahoru.
Tuto sílu může vyvinout např. raketový motor z mojí minulé pošty.
Chtěl jsem zjistit jestli se dá z této síly vypočítat potřebný výkon motoru.
To se mi nepodařilo, nenašel jsem k tomu žádné vzorce.
Proto jsem si řekl, že místo visení na místě nechám těleso oscilovat - padat a pomocí motoru znovu zvedat.
Práci pro zvednutí snadno vypočítám a přes tuto práci a čas dojdu k výkonu.
Potom budu zmenšovat amplitudu oscilací a tak se budu blížit k určité hodnotě výkonu.
Ale chyba! Čím menší amplituda, tím menší vychází výkon.
Takže při nekonečně malé amplitudě už těleso visí i bez přispění motoru.
Přitom říkáš, že tabulka je dobře? Tak kde je zakopaný pes?
Offline
#10 09. 03. 2017 10:36
Re: Visení vrtulníku
↑ Pega:
Dobře, tak ještě jednou (všechno toto už ti napsali ↑ edison: i ↑ LukasM: a je to krásně vysvětlené i v prvním odkazu od ↑ pietro:)
Na to, abys nějaké těleso udržel v klidu v určité výšce žádný výkon nepotřebuješ (a proto ti také vychází ta nula). Stačí to pověsit na strop nebo něčím podepřít.
mechanický výkon = práce za čas. Abys měl práci, musíš mít pohyb. Nemáš pohyb, nemáš práci.
Samozřejmě, pokud to "podpíráš" motorem (a jedno jestli vrtulník nebo raketa) , tak ten motor výkon mít bude. Ale ten výkon se odvíjí od toho, co se pohybuje (tj. u vrtulníku vzduch - prvním odkazu od ↑ pietro:, u rakety tryskající plyny).
Jenže tento výkon se odvíjí od parametrů konkrétního motoru, a ty neznáš.
Takže:
Chtěl jsem zjistit jestli se dá z této síly vypočítat potřebný výkon motoru.
Nedá.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#11 09. 03. 2017 10:38
Re: Visení vrtulníku
Pes je zakopán v tom, že správnost výpočtů nezaručuje, že počítají to, co chceš vypočítat.
U toho raketového motoru je to podobné, jen se to zjednoduší tím, že je u něj zavedena veličina zvaná specifický impulz a komplikuje tím, že princip činnosti obsahuje vyvrhování materiálu uskladněného v létacím stroji.
Takže skončíme u následující úvahy:
Bude-li Isp velký, bude malá spotřeba paliva [kg/s], ale ze stejného důvodu, jako u malé vrtule, bude potřeba velký výkon. A bude-li Isp malý, může být výkon libovolně malý, ale toho materiálu budeš muset pod sebe házet hodně:-)
Offline
#12 09. 03. 2017 10:42
Re: Visení vrtulníku
↑ Pega:
Tak znovu. Chyba je v tom, že oscilace a visení není totéž. Při visení (ať už je to vrtulník nebo o raketový motor) totiž těleso nikam nepadá a zase se nezvedá. Těleso prostě visí, a na to samo o sobě ještě není potřeba práce (stejně jako není potřeba konat práci k tomu, aby hrnek nepropadl stolem). Tvůj výpočet počítá jen se silami, které působí na to těleso, takže v mezním případě, kdy se těleso už nikam nehýbe, z něj přesně tohle vychází a je to tak správně. Tvůj výpočet pouze počítá práci potřebnou na neustálé zvedání tělesa o nějakou výšku, a ta je samozřejmě tím menší, o kolik méně to těleso zvedáš. Jakmile se přestane hýbat, bude vycházet nula.
Pokud je ten motor reaktivní, je ale ještě na místě se ptát, odkud se bere ta síla, která vyruší tíhovou. To ti tady už napsali tři lidé - klíčovou roli hraje něco, co ve svých výpočtech vůbec nemáš, a sice plyny unikající z toho raketového motoru. Motor tu potřebnou sílu generuje tak, že urychluje plyny na druhou stranu, a díky zákonu akce a reakce na něj tedy působí síla v opačném směru. Jako vedlejší produkt toho všeho tedy vznikne urychlený plyn, který má kinetickou energii, a tu mu ten motor musí dodávat. A ten plyn v tom modelu musíš mít.
Ještě jinak řečeno. Celý ten systém zahrnuje motor a unikající plyny. Výkon se spotřebovává na urychlení těch plynů, v důsledku kterého motor visí na místě. Ty sis z toho systému vzal tu část, která energii nespotřebovává (visící motor) a teď se divíš, že nespotřebovává energii.
Offline
#14 25. 09. 2017 06:31 — Editoval LukasM (25. 09. 2017 06:33)
Re: Visení vrtulníku
↑ Pega:
Nejsem si jistý, že to je ta samá otázka položená jinak. Každopádně na takové urychlování hmotného bodu je potřeba výkon 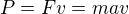 , kde v je okamžitá rychlost. Pro nulovou rychlost vychází nulový výkon, což je v souladu s tím, co ti tu pořád dokola všichni píšeme. Nicméně to stále není model, který by popisoval reaktivní motor.
, kde v je okamžitá rychlost. Pro nulovou rychlost vychází nulový výkon, což je v souladu s tím, co ti tu pořád dokola všichni píšeme. Nicméně to stále není model, který by popisoval reaktivní motor.
Offline
