Matematické Fórum

vanok · 08. 03. 2017 19:27

Pozdravujem,
Zda sa, ze vela ludi aspon poculo o Dedekind-ovej konstrukcii realnych cisiel. Tiez metoda Chauchy-ho postupnosti je dost znama.
No vsak su aj ine metody. Co viete o tom?

check_drummer

Ahoj,
sice další konstrukci neznám, ale nešlo by to pomocí vhodné axiomatiky? Např. existují tzv. tělesa reálného typu, pro které jeden z hlavních axiomů je, že neexistují čísla $a_i$ z tohoto tělesa taková, že $-1=\sum{a_i^2}$ . A nějakou další restrikcí bychom mohli získat přimo reálná čísla...

Ale nejsem si jist, zda tady zkoumáme reálná čísla jako model (jednu konkrétní množinu) a nebo reálná čísla jako strukturu popsanou nějakými axiomy - a taková struktura pak může mít více modelů, tedy nejen nám známá reálná čísla... To už by se ale rozběhla diskuse na téma, o kterém jsem tu kdysi psal - teorie vs. model a věta o neúplnosti...

vanok · 09. 03. 2017 21:09 — Editoval vanok (10. 03. 2017 04:39)

Ahoj,
Su aj ine, napr
http://alexandria.tue.nl/repository/fre … 597556.pdf
Alebo tu su popisane este dalsie
https://en.m.wikipedia.org/wiki/Constru … al_numbers

https://arxiv.org/pdf/1107.3688.pdf

A tu je popisany prehlad konstrukcii
https://arxiv.org/pdf/1506.03467.pdf

Pochopitelne vzdy treba dokazat, axiomy pre usporiadane teleso 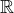$\Bbb R$ platia, a ze vsetki take telesa su isomorfne.

Matematické Fórum

#1 08. 03. 2017 19:27

Realne cisla

#2 09. 03. 2017 19:48 — Editoval check_drummer (09. 03. 2017 21:05)

Re: Realne cisla

#3 09. 03. 2017 21:09 — Editoval vanok (10. 03. 2017 04:39)

Re: Realne cisla

Zápatí