Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 03. 2017 22:25
Lokální extrémy (fce dvou proměnných)
Zdravím,
mám zadanou funkci: 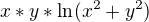
Vypočetl jsem druhé derivace, vytvořil jednotlivé matice druhých derivací. Avšak Sylvestrovo kritérium nemůžu využít. ve všech čtyřech případech mi vyšly determinanty nulové. Nevím přesně jak teď postupovat, jestli se v okolí tohoto bodu blížit a určovat okolní hodnoty nebo je lepší způsob. Jelikož druhá derivace není úplně primitivní. Zde přikládám své řešení. Výpočet determinantů tam nemám, ale jsou nulové. Mohl by mi někdo poradit jak dále postupovat popř. mě navést správným směrem? Děkuji Všem Filip.
Offline
#2 10. 03. 2017 00:14
Re: Lokální extrémy (fce dvou proměnných)
Ahoj ↑ Filip2142:,
to, že v těch čtyřech bodech není extrém mi připadá jasné z předpisu té funkce. Když si to představím na obrázku v polárních souřadnicích, je to jen 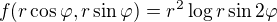 , takže malou změnou poloměru najdu v každém okolí každého stacionárního bodu dva jiné body, ve kterých bude hodnota menší a větší. Tzn., že to nemůžou být lok. extrémy.
, takže malou změnou poloměru najdu v každém okolí každého stacionárního bodu dva jiné body, ve kterých bude hodnota menší a větší. Tzn., že to nemůžou být lok. extrémy.
Dál se mi zdá, že jsi zapomněl na body 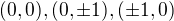 .
.
Offline
#3 10. 03. 2017 07:03
Re: Lokální extrémy (fce dvou proměnných)
↑ Filip2142:
Zdravím,
klidně jsi mohl pokračovat v původním tématu zde, protože z něho máš příslušné výpočty. A kdybys naopak zadal toto téma jako první, měl bys hned, podle návodu ↑ Bati:, pár stacionárních bodů " bez námahy" :-)
Offline
#4 10. 03. 2017 10:40 — Editoval Filip2142 (10. 03. 2017 10:46)
Re: Lokální extrémy (fce dvou proměnných)
↑ Bati:
Zdravím,
koukal jsem se na WA, kde právě tyto čtyři body bylo buď minima nebo maxima. Na ty další body bych přišel pohledem. O těch polárních ss jsem jen matně někde četl, mohl bys mi je případně trochu osvětlit? Podívám se mezitím sám na net. Opravdu tedy tyto nejsou extrémy? děkuji Filip.
WA: dole jsou vypsané exrémy:
Odkaz
Offline
#5 10. 03. 2017 15:55
Re: Lokální extrémy (fce dvou proměnných)
↑ Filip2142:
Ano, omlouvám se, máš pravdu. Myslel jsem si, že funkce 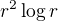 je rostoucí pro
je rostoucí pro  , ale není.
, ale není.
Offline
#6 10. 03. 2017 19:20
Re: Lokální extrémy (fce dvou proměnných)
↑ Filip2142:
Dobrý den.
Ty výpočty parciálních derivací tady ↑ Filip2142: nebudou v pořádku.
V uvedených čtyřech stacionárních bodech bude 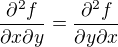 (obojí mi vyšlo = 0). S ohledem na symetrii zadané funkce vzhledem k proměnným x, y zřejmě nebude jedna ze zbývajících derivací (xx, yy) různá od nuly a druhá rovna 0 (tu už jsem se při výpočtu zamotal - ovšem je možno se podívat, co na to Wolfram: Odkaz).
(obojí mi vyšlo = 0). S ohledem na symetrii zadané funkce vzhledem k proměnným x, y zřejmě nebude jedna ze zbývajících derivací (xx, yy) různá od nuly a druhá rovna 0 (tu už jsem se při výpočtu zamotal - ovšem je možno se podívat, co na to Wolfram: Odkaz).
Hessiány nebudou rovny nule a dá se určit typ extrému (v uvedených čtyřech stacionárních bodech).
Pokud se tedy nemýlím.
Offline
#8 11. 03. 2017 10:53
Re: Lokální extrémy (fce dvou proměnných)
↑ Filip2142:
To mi připadá zbytečné, když už za nás někdo vymyslel obecnou metodu:
Druhé parciální derivace mi vyšly 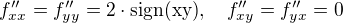
Takže Hessián  pro všechny uvedené stacionární body --> je v nich minimum nabo maximum (ne sedlový bod)
pro všechny uvedené stacionární body --> je v nich minimum nabo maximum (ne sedlový bod)
a v návaznosti na znaménko f''_{xx} tudíž je v uvedených čtyřech bodech ležících
- v prvním a třetím kvadrantu: minimum
- v druhém a čtvrtém kvadrantu: maximum
Takže ještě dořešit ostatní body (↑ Bati:).
Pokud se tedy nemýlím.
Offline
#9 11. 03. 2017 16:44 — Editoval Filip2142 (11. 03. 2017 17:13)
Re: Lokální extrémy (fce dvou proměnných)
↑ Jj:
Děkuji za reakci. Trochu nechápu ty Vaše druhé parciální derivace (hlavně s tou funkcí signum). A tu nerovnost u této matice také trochu nechápu. Děkuji za vysvětlení :)
Aha, tak jak vidím. Tak jsem se sekl v těch hodnotách v matici. Tak to ještě potom přepočtu.
Offline
#10 11. 03. 2017 18:05
Re: Lokální extrémy (fce dvou proměnných)
↑ Jj:
Až teď si uvědomuju, že jsem to s tou funkcí singnum napsal docela nejasně.
Funkcí sign(xy) rozumím funkci sign(x*y), kde x a y jsou souřadnice jednotlivých stacionárních bodů.
Druhé parciální derivace (podle xx i podle yy) ve stacionárních bodech vyšly v absolutní hodnotě shodně = 2, rozdíly jsou jen ve znaménkách. Tím jsem chtěl vlastně (jednoduše) vyjádřit to, že parciální derivace ve stacionárních bodech vyšly v návaznosti na rozmístění těchto bodů v jednotlivých kvadrantech takto:
kvadrant: 1 2 3 4
--------------------------------
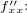 +2 -2 +2 -2
+2 -2 +2 -2
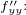 +2 -2 +2 -2
+2 -2 +2 -2
ale jenom jsem to domotal. Hessián v uvedených bodech je buď nebo
nebo  , tzn. jeho hodnota je v uvedených čtyřech stacionárních bodech vesměs > 0.
, tzn. jeho hodnota je v uvedených čtyřech stacionárních bodech vesměs > 0.
O využití Hessiánu k určování extrémů např. tady: Odkaz
Pokud se tedy nemýlím.
Offline
