Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » "Čísla" pokrývající rovinu (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 03. 2017 21:30
- check_drummer
- Příspěvky: 4766
- Reputace: 105
"Čísla" pokrývající rovinu
Ahoj,
existuje v rovině nespočetně mnoho disjunktních křivek ve tvaru číslice 0? A co ve tvaru číslice 8?
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#2 12. 03. 2017 21:48 — Editoval vanok (12. 03. 2017 23:22)
Re: "Čísla" pokrývající rovinu
Ahoj ↑ check_drummer:,
Odpoved je ano, pokial ide o"0", pokial ide o "8" neviem ( doeditovane)
Ale je ina otazka, je mozne tak vytvorit "particiu" roviny?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 12. 03. 2017 21:57
- check_drummer
- Příspěvky: 4766
- Reputace: 105
Re: "Čísla" pokrývající rovinu
↑ vanok:
Ahoj. Proč je odpověď ano i v případě číslic 8?
"Máte úhel beta." "No to nemám."
Offline
#4 12. 03. 2017 22:24 — Editoval vlado_bb (12. 03. 2017 22:42)
Re: "Čísla" pokrývající rovinu
↑ check_drummer: Nemala by kazda osmicka obsahovat vo svojom vnutri bod s obidvomi racionalnymi suradnicami? Nakolko vnutra oboch kruzkov osmicky su otvorene mnoziny a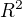 
je separabilny, povedal by som, ze ano, a teda odpoved na druhu cast otazky je nie.
edit: teda aspon pre "nie do seba zapadajuce" osmicky
Offline
#5 12. 03. 2017 23:04 — Editoval vanok (13. 03. 2017 11:11)
Re: "Čísla" pokrývající rovinu
Poznamka.
Slovo nespocetne iste znamena, ze ich kardinal je vädci ako ten mnoziny 
?
Vtedy som potom priliz rychlo odpovedal: pre "8" nemam argument.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 13. 03. 2017 10:10 — Editoval vanok (14. 03. 2017 18:37)
Re: "Čísla" pokrývající rovinu
Myslienka od ↑ vlado_bb: umoznuje kazdej "8" priradit jedno rationalne cislo. Tak kazda taka "rodina" takych kriviek moze byt indexovana rationalnymi cislami... ( edit: skor vhodnymi dvojicami rationalnych dvojic) a tak musi byt spocetna ( vo zmysle ↑ vanok: ako tu).
Edit. Pozor, ↑ vlado_bb: dve do seba zapadujuce "8" nemozu by disjunktne
Pre "0" mozme uvazovat napr. urcite "rodiny" sustrednych kruznic...
Co sa tyka pokrytia roviny, tak na to ( intuitivne) odpoved je nie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 14. 03. 2017 17:53
- check_drummer
- Příspěvky: 4766
- Reputace: 105
Re: "Čísla" pokrývající rovinu
↑ vlado_bb:
Ahoj, i pro ty osmičky, které jsou částí smyčky větší osmičky to platí - stačí každé osmičce přiřadit dva body s racionálními souřadnicemi - každý bod z jiné smyčky. A žádné dvě osmičky nemohou sdílet stejnou dvojici takovýchto bodů a bodů je jen spočetně...
"Máte úhel beta." "No to nemám."
Offline
#8 14. 03. 2017 19:23
:)
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » "Čísla" pokrývající rovinu (TOTO TÉMA JE VYŘEŠENÉ)