Matematické Fórum

Hanuna2

Dobry den,
mam priklad:

$t(x^{2}+1)-3=x(x-2t)$

po upravach mi vyjde:

$x^{2}(t-1)+2tx+t-3=0$

Dosadim do zorec pro výpočet kořenů kvadratické rovnice:

$\frac{-2t\pm \sqrt(2t){^{2}-4(t-1)(t-3)}}{2(t-1)}$

nesmim delit 0, musi byt splneno t-1≠0, t≠1
zjistim, pro ktera x plati, ze t =1, dosadim do rovnice $x^{2}(t-1)+2tx+t-3=0$ a vychazi mi, x=1

upravim kvadratickou rovnici a vychazi mi: $\frac{-1\pm \sqrt{4t-3}}{t-1}$

Dale pocitam, kdy je D>0
4t-3>0
t>3/4 t∈(3/4;∞)∖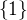 $\{1\}$ $K=\frac{-1\pm \sqrt{4t-1}}{t-1}$

D<0
t <3/4 t∈(-∞;3/4) K=∅

4t-3=0
t=4/3 dosadim do kvadraticke rovnice a vyjde mi, ze x=4

Zaver:
- t =1 K={1}
- t∈(3/4;∞)\{1\}
$K=\frac{-1\pm \sqrt{4t-1}}{t-1}$

- t <3/4 t∈(-∞;3/4) K=∅
- t=3/4 K=4

Je to spravne?

H

vanok · 16. 03. 2017 12:02 — Editoval vanok (16. 03. 2017 13:57)

Ahoj ↑ Hanuna2:,
Dobra metoda, je trochu skoda, ze chybaju podrobnosti vo vypoctoch.
Inac presny zapis v latexe ma byt
$\frac {-2t\pm \sqrt{(2t)^{2}-4(t-1)(t-3)}}{2(t-1)}$

Edit. Opraveny moj nepresny prispevok.

Hanuna2 · 16. 03. 2017 12:18

Dobry den,
dekuji Vam za reakci, ale moc Vam nerozumim, kde mam chybu... cislo 4 myslite jako x? To jsem si myslela ze mam vyreseno uvahou D=0, tedy vysledek t=3/4 K=4.
H

vanok · 16. 03. 2017 13:21 — Editoval vanok (16. 03. 2017 13:42)

↑ Hanuna2:,
Vypocitaj $(2t)^{2}-4(t-1)(t-3)=...$

Edit.
Prepac, z casti mas pravdu.
Teraz som si vsimol, ze tvoj vypocet D je spravny, to ma pomylilo je, ze pises hotove odpovede bez vypoctov ktore k tomu vedli.

A asi preto tvoj vypocet pre t=4/3 je chybny
Dalsia vec co mozes zlepsit je zapis K=... Ak ide o mnozinu rieseni to treba doslednejsie napisat.
Ako?

Tiez ked pises tvoj komentar, by bolo dobre pridat slovny doprovod.

( nikdy netreba miesat nejaku mnozinu a jej prvky: pohar vody, nie je to iste ako voda ....)

Al1 · 16. 03. 2017 13:22

↑ Hanuna2:

Zdravím,

$x^{2}(t-1)+2tx+t-3=0$ řešíš
A jestliže t-1=0, potom řešíš lineární rovnici s řešením x=1
B jestliže t≠1, potom řešíš kvadratickou rovnici:
a) D>0 máš správně interval, ale tvé řešení $\frac{-1\pm \sqrt{4t-3}}{t-1}$ je chybné, správně je $x_{1,2}=\frac{-t\pm \sqrt{4t-3}}{t-1}$
b) D=0, řešíš 4t-3=0, ale tvé řešení je chybné, správně t=3/4 a je nutné opravit x.

A jen doporučení:
nepiš do závěru
-t, ono to vypadá, že máš podmínky pro minus t. A ona to má být spíše odrážka, že?

Hanuna2 · 16. 03. 2017 13:36

Vypocet

$(2t)^{2}-4(t-1)(t-3)= 4t^{2}-4[(t-1)(t-3)]= 4t^{2}-4(t^{2}-3t-t+3)= 4t^{2}-4(t^{2}-4t+3= 4t^{2}-4(t^{2}-4t+3)=$

$4t^{2}-4t^{2}+16t-12= 16t-12$

H

Hanuna2 · 16. 03. 2017 13:46

Aha, uz to vidim,

$x_{1,2}=\frac{-t\pm \sqrt{4t-3}}{t-1}$

je resenim kvadraticke rovnice.

b)D=0 resim 4t-3=0, a resenim je x=3, tzn. t=3/4 K=3

Ano, ma to byt odrazka. Jiz to nebudu pouzivat, at to neni zavadejici.

Dekuju.
H

vanok · 16. 03. 2017 13:47

↑ Hanuna2:,
Vyborne, co ti doporucujem je uzitocne pisat podrobnejdie tvoje postupy riesenia.

Co sa tyka rieseni, pis mnozina realnych rieseni je K ={....}, alebo realne riesenia su ... (Ak t .....)
Staci?

Otazka, komplexne riesenia ste nevideli?

vanok · 16. 03. 2017 13:51 — Editoval vanok (16. 03. 2017 14:03)

↑ Hanuna2:,
Presne pis mnozina rieseni je K={3} ak t=3/4

Alebo riesenie rovnice je x=3, ak t=3/4

Vidis.

Tiez treba pisat
Mnozina rieseni je
$K={ \frac{-1\pm \sqrt{4t-1}}{t-1} }$ .....
Alebo riesenia rovnice su $x_{1,2}=\frac{-1\pm \sqrt{4t-1}}{t-1}$ ...

Hanuna2 · 16. 03. 2017 14:39

Dekuju za konzultaci s prikladem.
H

vanok · 16. 03. 2017 15:51

👍 dobre pokracovanie a uspechy.

Matematické Fórum

#1 16. 03. 2017 11:02 — Editoval Hanuna2 (16. 03. 2017 11:22)

Kvadraticka rovnice s paramatrem

#2 16. 03. 2017 12:02 — Editoval vanok (16. 03. 2017 13:57)

Re: Kvadraticka rovnice s paramatrem

#3 16. 03. 2017 12:18

Re: Kvadraticka rovnice s paramatrem

#4 16. 03. 2017 13:21 — Editoval vanok (16. 03. 2017 13:42)

Re: Kvadraticka rovnice s paramatrem

#5 16. 03. 2017 13:22

Re: Kvadraticka rovnice s paramatrem

#6 16. 03. 2017 13:36

Re: Kvadraticka rovnice s paramatrem

#7 16. 03. 2017 13:46

Re: Kvadraticka rovnice s paramatrem

#8 16. 03. 2017 13:47

Re: Kvadraticka rovnice s paramatrem

#9 16. 03. 2017 13:51 — Editoval vanok (16. 03. 2017 14:03)

Re: Kvadraticka rovnice s paramatrem

#10 16. 03. 2017 14:39

Re: Kvadraticka rovnice s paramatrem

#11 16. 03. 2017 15:51

Re: Kvadraticka rovnice s paramatrem

Zápatí