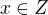Matematické Fórum

aniuce · 22. 02. 2017 16:24

Dobrý den potřebuji pomoct vyřešit
rozdíl čtverců 2 celých čísel je roven 24, najděte tato čísla

x^2-y^2=24

přišla jsem na čísla 5,1 a 7,5 ale potřebovala bych nějak zjistit interval, aby mi to omezilo, která čísla můžu dosadit
děkuji

vanok · 22. 02. 2017 17:50

Ahoj ↑ aniuce:,
Napis podrobne tvoje riesenie.
Poznamka.
Akoze hladas cele riesenia, nezabudni na negativne riesenia.
Ako napr. x=-5,y=1.

vlado_bb

↑ aniuce:Vsimni si rozdiely druhych mocnin dvoch po sebe iducich celych cisel. Ak je rozdiel cisel $100^2$ a $101^2$ vacsi ako $24$ , tak zrejme uz aj rozdiel $100^2$ a $z^2$ , kde $z>101$ bude vacsi ako 24.

misaH · 22. 02. 2017 18:04 — Editoval misaH (22. 02. 2017 18:27)

Toto nepomôže?:

$(x-y)(x+y)=24$

A súčasne

$24=3\cdot 2\cdot 2\cdot 2\cdot 1$

A ako píše vanok, uvážiť aj záporné činitele.

Potom stačí vyriešiť zopár sústav rovníc a je to ... :-)

vanok · 22. 02. 2017 18:41

👍↑ misaH:

misaH · 22. 02. 2017 19:48

↑ vanok:

:-)

Veľmi pekne ďakujem...

vanok · 22. 02. 2017 21:36

Poznamka.
Ak niekto chce vediet viac na tuto temu ako aj suvisiace veci, je dobre si precitat "histoire of the theory of numbers dickson" ( vsetki tri diele).

aniuce · 23. 02. 2017 09:42 — Editoval aniuce (23. 02. 2017 09:47)

děkuji
já to udělala takhle:

$y=\mp \sqrt{x^{2}-24}$
z toho

$x^{2}-24\ge 0;$

takže

$x\ge \mp 2\sqrt{6}$

takže když experimentem dosazuji hodnoty od 5 a víš (plus mínus zatím nechám to vím že pak přidám) tak mi vyjde x=5 a y=1 a také x=7,y=5, to vím že vyjde, i jsem si to zkoušela do tabulky a odčítat, pak už jsou rozdíly moc velký, ale nevím jak to zapsat abych udělala například že x<10, abych to omezila i zhora, napadá mě akorát x>y ale to pak nevím jak dát dohromady
tak jestli poradíte
děkuji

vanok · 23. 02. 2017 11:17 — Editoval vanok (23. 02. 2017 11:18)

Ahoj ↑ aniuce:,
Je vela moznych metod na riesenie.
Jedna z metod ↑ misaH: vyuzije rozklad cisla 24.
Staci vyuzit vsetki rozklady na dva kladne faktory. ( ine riesenia, ktore maju aspon jednu cast negativnu, potom doplnis malou uvahou)
24 (=a.b)
=24.1
=12.2
=8.3
=6.4
.... napis vsetki moznosti.

Potom vyuzi, ze tvoja rovnica sa da napisat (x+y)(x -y)=24, a x+ y>x-y pre kladne x,y. Tiez nezabudni, ze hladame v tejto etape len cele kladne riesenia.
Preto staci vysetrit tieto sustavy
Prvaz nich:
x+y=24
x-y=1

Autor skryl část textu. Zobrazit/skrýt!

.... treba pokracovat...

Al1 · 23. 02. 2017 11:17

↑ aniuce:

Zdravím,

z $x^{2}-24\ge 0$ plyne ovšem $|x|\ge 2\sqrt{6}$ . A když x je navíc celé číslo, vybíráš ho z množiny $\{\ldots -7; -6; -5; 5; 6; 7\ldots \}$

Honzc · 23. 02. 2017 11:24 — Editoval Honzc (23. 02. 2017 11:26)

↑ aniuce:
Omezit shora to můžeš takto:
Předpokládejme, že x,y>0 a zátoveň x>y.
Pak pro celá čísla může být minimální rozdíl x-y=1
Dosadíme do původní rovnice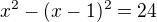
$x^{2}-(x-1)^{2}=24$
dostaneme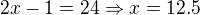
$2x-1=24\Rightarrow x=12.5$
a tedy 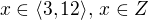$x\in \langle3,12\rangle,\,x\in Z$

Autor skryl část textu. Zobrazit/skrýt!

Poznámka: "víš" se píše výš

misaH · 23. 02. 2017 11:41 — Editoval misaH (23. 02. 2017 12:19)

↑ aniuce:

Úplne zbytočné.

24 = 1.24=2.12=3.8=4.6

Teda riešiš sústavy

x-y=1
x+y=24

Netreba, lebo evidentne nevyjde celé číslo.

x-y=2
x+y=12

Vyjde 7 a 5. Takmer spamäti.

x-y=3
x+y=8

Netreba.

x-y=4
x+y=6

Vyjde 5 a 1.

A potom už len

24=(-1)(-24)=(-2)(-12)=(-3)(-8)=(-4)(-6)

Znova sústavy (pozor na to, ktoré číslo patrí k x-y a ktoré k x+y).

Opäť dve sústavy ani nebude treba riešiť.

Žiadne iné možnosti neexistujú.

Úplne jednoduché riešenie, nechápem, načo sa paprať s obmedzeniami a čo ja viem s čím.

No ale samozrejme, ako chceš... Prečo robiť veci jednoducho, však?

vanok · 23. 02. 2017 12:24 — Editoval vanok (23. 02. 2017 12:26)

↑ misaH:,
Poznamka.
Je este rychlejsie.
Ked sa uz najdu tie dve dvojice kladnych rieseni, vsetki ostante sa mozu nast vdaka znamej identite 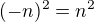$(-n)^2=n^2$ .
Kontrola

Autor skryl část textu. Zobrazit/skrýt!

aniuce · 23. 02. 2017 14:10

Děkuji, už to asi dám nějak dohromady

vlado_bb · 23. 02. 2017 14:54

↑ aniuce: Verim ze to uz zvladnes, ale predsa len este jedna poznamka: zapis $x \ge \mp 2\sqrt{6}$ ktory pouzivas, je pomerne nezmyselny a moze ti raz sposobit problemy. Ide o to, ze na oboch stranach znamienka $\ge$ by mali byt cisla. Kym $x$ cislo je, $\mp 2\sqrt{6}$ cislo nie je.

aniuce · 17. 03. 2017 15:46

díky

Matematické Fórum

#1 22. 02. 2017 16:24

celá čísla

#2 22. 02. 2017 17:50

Re: celá čísla

#3 22. 02. 2017 17:56 — Editoval vlado_bb (22. 02. 2017 17:57)

Re: celá čísla

#4 22. 02. 2017 18:04 — Editoval misaH (22. 02. 2017 18:27)

Re: celá čísla

#5 22. 02. 2017 18:41

Re: celá čísla

#6 22. 02. 2017 19:48

Re: celá čísla

#7 22. 02. 2017 21:36

Re: celá čísla

#8 23. 02. 2017 09:42 — Editoval aniuce (23. 02. 2017 09:47)

Re: celá čísla

#9 23. 02. 2017 11:17 — Editoval vanok (23. 02. 2017 11:18)

Re: celá čísla

#10 23. 02. 2017 11:17

Re: celá čísla

#11 23. 02. 2017 11:24 — Editoval Honzc (23. 02. 2017 11:26)

Re: celá čísla

#12 23. 02. 2017 11:41 — Editoval misaH (23. 02. 2017 12:19)

Re: celá čísla

#13 23. 02. 2017 12:24 — Editoval vanok (23. 02. 2017 12:26)

Re: celá čísla

#14 23. 02. 2017 14:10

Re: celá čísla

#15 23. 02. 2017 14:54

Re: celá čísla

#16 17. 03. 2017 15:46

Re: celá čísla

Zápatí