Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 03. 2017 13:39
Izomorfismus Booleových algeber
Mohl by mi prosím někdo pomoct s tímto příkladem nebo alespoň naťuknout jak na to.. Mockrát děkuju
Nechť g : Y → Z je bijekce mezi konečnými množinami. Zobrazení g indukuje zobrazení 2^g : 2^Y → 2^Z,, dané předpisem
2^g (A) = {g(a) : a ∈ A}, pro libovolné A ⊆ Y . Ukažte, že 2^g je isomorfismus Booleových algeber (2^Y, ⊆)
a (2^Z, ⊆).
Offline
#2 14. 03. 2017 15:01
Re: Izomorfismus Booleových algeber
↑ hradil11:
Ahoj. Pátral bych po přesných definicích těch pojmů.
Offline
#3 14. 03. 2017 15:13
Re: Izomorfismus Booleových algeber
↑ Rumburak: to jsem se pokoušel a i tak stale netuším, jak mam ukázat, že je to izomorfismus...
Offline
#4 14. 03. 2017 15:56
#5 14. 03. 2017 17:16
Re: Izomorfismus Booleových algeber
↑ vlado_bb:↑ vlado_bb: Isomorfismus uspořádaných množin (X,  ) a (Y,
) a (Y,  ) je bijekce f :X → Y taková, že pro každé a, b ∈ X platí a
) je bijekce f :X → Y taková, že pro každé a, b ∈ X platí a  b právě když f(a)
b právě když f(a) 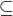 f(b). Tyto uspořádané množiny jsou isomorfní (psáno (X,
f(b). Tyto uspořádané množiny jsou isomorfní (psáno (X,  )
) 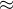 (Y,
(Y, 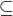 )), pokud mezi nimi existuje isomorfismus.
)), pokud mezi nimi existuje isomorfismus.
Offline
#6 14. 03. 2017 17:17
#7 14. 03. 2017 19:18 — Editoval vlado_bb (14. 03. 2017 19:19)
Re: Izomorfismus Booleových algeber
↑ hradil11: Spravne, teda az na to, ze v mnozine  mame zrejme relaciu
mame zrejme relaciu 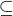 . Takze
. Takze 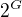 musi byt bijekcia s akousi vlastnostou, tej sa budeme venovat neskor. Skus zacat tym, ze dokazes, ze ide o bijekciu.
musi byt bijekcia s akousi vlastnostou, tej sa budeme venovat neskor. Skus zacat tym, ze dokazes, ze ide o bijekciu.
Offline
#8 14. 03. 2017 19:29
#9 14. 03. 2017 19:43
#10 14. 03. 2017 20:07
Re: Izomorfismus Booleových algeber
↑ vlado_bb: bijekce je teda zobrazení, které je surjektivní (všechny obrazy mají vzor), injektivní ( 1 obraz má 1 vzor) ... ale jak to mám dokázat na tomto konkrétním příkladu
Offline
#11 15. 03. 2017 06:18
Re: Izomorfismus Booleových algeber
↑ hradil11: Zacni napriklad injektivnostou. Ta hovori, ze dva rozne vzory maju aj rozne obrazy. Napis si teda, co znamena, ze dva vzory su rozne a ukaz, ze potom aj obrazy su rozne.
Offline
