Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 03. 2017 20:09
Offline
#3 29. 03. 2017 20:51
Re: Vyjadrenie postupnosti
↑ vytautas: No praveze by som to potrebovala dat do jedneho vzorca pre akekolvek n...ak sa to vobec da.
Offline
#4 29. 03. 2017 23:42
Re: Vyjadrenie postupnosti
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 30. 03. 2017 09:46
Re: Vyjadrenie postupnosti
Ahoj ↑ green19:,
Napr. vdaka https://en.m.wikipedia.org/wiki/Polynom … erpolation
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 30. 03. 2017 11:39
Re: Vyjadrenie postupnosti
↑ green19:
Stačí nalézt polynom ![kopírovat do textarea $P(x)\in\mathbb Z_7[x]$](/mathtex/15/150a6d03cf974d2c96f4bf786b01f693.gif) tak, aby
tak, aby
Stačí použít základy modulární aritmetiky.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 30. 03. 2017 12:58
Re: Vyjadrenie postupnosti
↑ green19:Jestli není úkolem opravdu přímo ten vzorec a potřebujete to na něco jiného (jako, co já vím, limitu), pak vzorec skoro určitě není tou správnou cestou. Existují i jiné elementární vzorce než pomocí modulo, třeba lineární kombinace funkcí  (což ovšem vyžaduje vyřešit soustavu šesti rovnic o šesti neznámých s iracionálními koeficienty) nebo lze šikovně užít funkce
(což ovšem vyžaduje vyřešit soustavu šesti rovnic o šesti neznámých s iracionálními koeficienty) nebo lze šikovně užít funkce  a funkci signum ke konstrukci obecného vzorce, do kterého jen dosadíte prvních šest členů posloupnosti a vzorec z nich udělá periodu. Ve všech přípdech je ale výsledný vzorec tak složitý, že jakákoli práce s ním je velmi obtížná.
a funkci signum ke konstrukci obecného vzorce, do kterého jen dosadíte prvních šest členů posloupnosti a vzorec z nich udělá periodu. Ve všech přípdech je ale výsledný vzorec tak složitý, že jakákoli práce s ním je velmi obtížná.
Offline
#9 30. 03. 2017 13:21
Re: Vyjadrenie postupnosti
↑ Cynyc:
Obávám se, že v tomto je situace ještě horší. Těch rovnic bude 7, počátečních podmínek je totiž 7. Posloupnost je samozřejmě dána diferenční rovnicí  . Pracovat s lineární kombinací funkcí
. Pracovat s lineární kombinací funkcí  chce značnou dávku odvahy.
chce značnou dávku odvahy.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 30. 03. 2017 18:27 — Editoval vanok (31. 03. 2017 01:07)
Re: Vyjadrenie postupnosti
Ahoj ↑ Pavel:,
Langrangove interpolacne polynomy prisposobene na dane teleso sa daju pouzit.
Edit. Co da:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 30. 03. 2017 21:46
Re: Vyjadrenie postupnosti
↑ Pavel: Oj, jak vidím, práce kvapná, málo platná: jednak jsem přehlédl, že opakující se část končí až nulou, takže perioda je 7, a jednak napsal nesmysl, lineární kombinaci je třeba dělat z  , jinak by to nemělo příslušnou periodu. U
, jinak by to nemělo příslušnou periodu. U  jsem nepsal o lineární kombinaci, ale o použití signum, kterým lze snadno vyrobit charakteristické funkce zbytkových tříd modulo 7.
jsem nepsal o lineární kombinaci, ale o použití signum, kterým lze snadno vyrobit charakteristické funkce zbytkových tříd modulo 7.
Offline


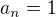 ak
ak 
 ak
ak 
 inak
inak