Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 27. 04. 2017 20:13 — Editoval vlado_bb (27. 04. 2017 20:15)
Re: Jsou dané množiny podprostory?
↑↑ Filip2142: Ano, mohol si napriklad vziat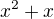 
a vynasobit dvomi (alebo, este lepsie, nulou) a mal by si to tiez dokazane.
Ale teraz, ked si uz ukazal, ze sucet dvoch prvkov 
do nej nemusi patrit, tak uz nie!!!!! Ak uz nieco dokazeme, tak preco by som to preboha dokazoval "este viac"?
Ine je samozrejme ak najdeme dva principialne rozne dokazy toho isteho, co je aj tento pripad, teda pomocou suctu aj nasobku. Ale tam jasne povieme, ze ide o dva rozne dokazy. Prezentovat to ako jeden dokaz by mohlo znamenat, ze sme si nevsimli ze uz je vec vyriesena a omylom pokracovali dalej.
Offline
#27 27. 04. 2017 20:18
Re: Jsou dané množiny podprostory?
↑ vlado_bb:
Jasně, to by taky nedělalo dobrotu a vypadal bych řekněme, jako hlupák...
Teď k tomu druhému příkladu, nulový vektor pro tu podmínku platí a vybrat si zase polynomy a sečíst a už teď je vidět, že to platí...
Offline
#28 27. 04. 2017 20:22
Re: Jsou dané množiny podprostory?
↑ Filip2142: Ano, tam je to evidentny podpriestor. Technicke detaily uz zvladnes. Inak, vsimni si, ze v tejto suvislosti je jedno, ci hovorime o polynomoch 
alebo o trojiciach ![$[a,b,c]$](/mathtex/3b/3b30c780b380163d666cdf1b11a7baff.gif "kopírovat do textarea")
. Sucty aj nasobky sa spravaju rovnako. Spomen si na to, ked budete preberat izomorfizmy linearnych priestorov.
Offline