Matematické Fórum

Senior · 09. 05. 2009 10:08

Je dán poloměr kružnice vepsané a velikost přepony v pravoúhlém trojúhelníku. Vím, že úloha může mít 4 řešení, vím, že hledaný vrchol bude ležet na Tháletově kružnici, vím že hledám tečnu, ale nemůžu s řešením hnout. Díky za pomoc. Honza.

amatika · 12. 05. 2009 00:50

↑ Senior:
Neviem, či je to tou neskorou hodinou, ale nejako sa mi z tvojho textu nedarí zistiť, čo vlastne treba vypočítať, zistiť, vyjadriť....

mák · 12. 05. 2009 07:02

Pokud znáš pouze přeponu (strana c) u pravoúhlého trojúhelníka
a poloměr kružnice vepsané (r), pak platí: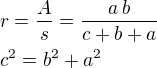

$r=\frac{A}{s}=\frac{a\,b}{c+b+a}\nl{c}^{2}={b}^{2}+{a}^{2}$

Řešením obou rovnic lze vypočítat neznámé a i b

$a_1=-\frac{\sqrt{-4\,{r}^{2}-4\,c\,r+{c}^{2}}-2\,r-c}{2},\,\,b_1=\frac{r\,\sqrt{-4\,{r}^{2}-4\,c\,r+{c}^{2}}-2\,{r}^{2}-3\,c\,r}{\sqrt{-4\,{r}^{2}-4\,c\,r+{c}^{2}}-c}\nla_2=\frac{\sqrt{-4\,{r}^{2}-4\,c\,r+{c}^{2}}+2\,r+c}{2},\,\,b_2=\frac{r\,\sqrt{-4\,{r}^{2}-4\,c\,r+{c}^{2}}+2\,{r}^{2}+3\,c\,r}{\sqrt{-4\,{r}^{2}-4\,c\,r+{c}^{2}}+c}$

Pro ověření jsem dosadil za stranu (přeponu) c = 10 a poloměr (vepsané kružnice) r = 2.
Vychází odvěsny a = 8 a b = 6

Podobně by to mělo jít i pro obecný trojúhelník. Bude potřeba však zadat ještě navíc úhel gamma.

Senior · 12. 05. 2009 10:08

↑ amatika:Díky za odpověď . Ale zadání je " sestrojit pravoúhlý trojúhelník, kde je zadána délka přepony a poloměr kružnice vepsaané ".
Díky za případnou pomoc. Honza.

Matematické Fórum

#1 09. 05. 2009 10:08

Kružnice vepsaná a přepona

#2 12. 05. 2009 00:50

Re: Kružnice vepsaná a přepona

#3 12. 05. 2009 07:02

Re: Kružnice vepsaná a přepona

#4 12. 05. 2009 10:08

Re: Kružnice vepsaná a přepona

Zápatí