Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analitická geometrie - vzájemná poloha přímek (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 05. 2017 10:29 — Editoval stitch123 (08. 05. 2017 10:44)
Analitická geometrie - vzájemná poloha přímek
Zdravím!
V zadání jsou dvě přímky: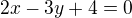
a 
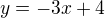
Mám zjistit jejich vzájemnou polohu (prý jsou to různoběžky). Vím, jak podobnej příklad spočítat, kdyby byla jedna z nich zadána parametricky, ale takhle si nejsem jistej.
Dosadil jsem Y z druhé přímky do první a spočítal, že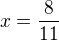 
, následně 
.
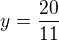Je mi to k něčemu?
Offline
- (téma jako vyřešené označil(a) stitch123)
#2 08. 05. 2017 10:32 — Editoval misaH (08. 05. 2017 10:37)
- misaH
- Příspěvky: 13459
Re: Analitická geometrie - vzájemná poloha přímek
↑ stitch123:
(Analytická...)
Výsledok som nekontrolovala. (Môžeš urobiť skúšku alebo nechať skontrolovať cez Wolfram alpha.)
Metóda je dobrá.
Každá rovnica predstavuje súradnice bodov roviny, ktoré na priamke ležia.
Priesečník leží na obidvoch priamkach, teda jeho súradnice musia vyhovovať jednej aj druhej rovnici.
Nájsť priesečník znamená vyriešiť sústavu.
Offline
#4 08. 05. 2017 10:50 — Editoval stitch123 (08. 05. 2017 10:53)
Re: Analitická geometrie - vzájemná poloha přímek
Takže průsečík je ![$X[\frac{8}{11};\frac{20}{11}]$](/mathtex/e6/e610ccce4599d1a6f906faabbb749b9c.gif "kopírovat do textarea")
, tzn. přímky mají jeden průsečík => různoběžné? Co by mi vyšlo, kdyby to byly totožné nebo rovnoběžné přímky?
EDIT: Tento bod X vyhovuje oběma rovnicím. Po dosazení vychází 0. Kdyby nevyhovoval, znamenalo by to, že nemají průsečík, tudíž jsou to rovnoběžky, mám pravdu?
Offline
#5 08. 05. 2017 10:51
#7 08. 05. 2017 10:59 — Editoval misaH (08. 05. 2017 10:59)
- misaH
- Příspěvky: 13459
Re: Analitická geometrie - vzájemná poloha přímek
↑ stitch123:
Ahoj.
:-)
Rep netreba, ale dík.
Naschvál som poslala odkaz, pre kontrolu je to dobrá vec, aj keď nefunguje úplne stopercentne a niektoré označenia má iné než sú naše zvyky.
V tejto úlohe je možné relatívne ľahko urobiť skúšku... :-)
Offline
#8 08. 05. 2017 11:04
Re: Analitická geometrie - vzájemná poloha přímek
↑ stitch123:
Zdravím,
společné body dvou přímek hledáš vyřešením soustavy sestavené z jejich rovnic.
Pokud má taková soustava jedno řešení, pak jsou přímky různoběžné. Pokud má soustava nekonečně mnoho řešení, pak jsou to shodné rovnoběžky. Pokud nemá žádné řešení, pak jsou to rovnoběžky různé.
Když ti vyjde jeden společný bod a nevyjde zkouška, pak buď jsi průsečík chybně spočítal, ale přímky jsou různoběžné, nebo jsi celkově chybně počítal- průsečík neměl být žádný, přímky by byly robnoběžné různé.
Pokud se ti nejedná o spočítání průsečíku, ale chceš znát vzájemnou polohu, stačí se podívat např. na směrnicové rovnice obou přímek. Různoběžky mají různé směnice, např. y=x+3, y=-x+3, rovnoběžné přímky mají směrnici stejnou, např. y=2x-1, y=2x+1. Totožné přímky mají shodné celé rovnice, např. y=-3x+5, y=-3x+5
Offline
#10 08. 05. 2017 11:15
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analitická geometrie - vzájemná poloha přímek (TOTO TÉMA JE VYŘEŠENÉ)