Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 05. 2017 18:26
Laurentův rozvoj
Dobrý den,
chtěl bych poprosit o pomoc, kde dělám v příkladu na konci chybu.
Rozdělím na parciální zlomky:
Budu užívat tento vzorek:
Udělám zvlášť první a druhý zlomek a dostanu:
Pokud bude n sudé, pak suma bude nulová, pokud bude n liché, tak závorka mi dá -2 a zkrátím to s 2 ve jmenovateli ... jenže nejsem schopen se dostat k výsledku, který je v zadáání.
Děkuji za radu.
Offline
- (téma jako vyřešené označil(a) s-o-k-o-l)
#2 09. 05. 2017 11:27 — Editoval Rumburak (09. 05. 2017 12:01)
Re: Laurentův rozvoj
↑ s-o-k-o-l:
Ahoj. Jdeš na to, myslím, zbytečně složitě. Využil bych následující poznatek:
Pro  položme
položme 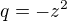 , kde rovněž
, kde rovněž  , takže nekonečná geometrická řada
, takže nekonečná geometrická řada  je konvergentní a má součet
je konvergentní a má součet
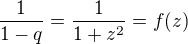 .
.
Takže celkem
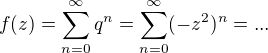
a upravit do standardního tvaru mocninné řady se středem v bodě 0, která zde bude zároveň
hledanou Laurentovou řadou.
Offline
#3 09. 05. 2017 12:31 — Editoval s-o-k-o-l (09. 05. 2017 12:31)
Re: Laurentův rozvoj
↑ Rumburak:
Díky moc ... to je o dost lehčí. A pro případ, kdy mám absolutní hodnotu větší jak 1 ... postupuji korektně?
Mám problém upravit hranici, odkud kam jde suma.
Offline
#4 09. 05. 2017 14:04 — Editoval Rumburak (09. 05. 2017 14:46)
Re: Laurentův rozvoj
↑ s-o-k-o-l:
Tan samotný rozvoj pro případ  (opraveno) je v podstatě správně (až na vloženou rovnost
(opraveno) je v podstatě správně (až na vloženou rovnost  ,
,
která do tohoto řetězce rovností nepatří a navíc je i v daném kontextu chybná: zde totiž je  ).
).
Terminologicky zde ovšem nejde o LR se středem v bodě 0, ale o LR se středem v bodě  .
.
(Ještě by bylo vhodné řadu upravit do jednoduššího tvaru, aby tam výraz  nebyl dvakrát.
nebyl dvakrát.
viz přesný tvar LŘ dle její definice).
Offline
#6 10. 05. 2017 14:10 — Editoval Rumburak (10. 05. 2017 14:13)
Re: Laurentův rozvoj
↑ s-o-k-o-l:
Ještě doplním: LŘ vhodné funkce  se středem v bodě
se středem v bodě  má, pokud existuje, obecný tvar
má, pokud existuje, obecný tvar
(1)  ,
,
kde 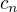 jsou čísla závislá příslušným způsobem na funkci
jsou čísla závislá příslušným způsobem na funkci  . Je-li funkce
. Je-li funkce  navíc holomorfní
navíc holomorfní
v bodě  , pak pro
, pak pro  je
je  a řada (1) má tvar
a řada (1) má tvar
(2)  .
.
V tomto smyslu je nutno brát mé předchozí komentáře.
Dopručuji projít si teorii v příslušných studijních materiálech
Offline