Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 05. 2009 16:10
Posloupnosti
hoj pomůžete mi zase? :-)
1. Urči oč je součet prvých 100 přirozených čísel sudých větší než součet prvých 100 přirozených čísel lichých. Tenhle příklad mám vyřešen prakticky, ale potřeboval bych ho tou teoretickou cestou.
2. Mezi kořeny rovnice x^2 + x - 12 = 0 vložte 13 členů tak, aby s kořeny rovnice tvořila 15 členů aritmetické posloupnosti. Vypište je.
3. V aritmetické posloupnosti je a1 = 3 , d = 2. Kolik členů dává součet Sn= 120?
4. V aritmetické posloupnosti je a1 = 30, d = -3, urči člen, který se rovná osmině součtu všech členů předcházejících.
5. Součet prvých devíti členů aritmetické posloupnosti je 108. Urči je, víme, že se jedná o čísla přirozená.
Offline
#2 11. 05. 2009 16:24
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Posloupnosti
1)
sudé číslo: 2k (k náleží N)
liché číslo: (2l - 1) (l náleží n)
Spočítáme součty:
Teď zkus to samé pro lichá čísla.
2)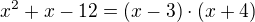
Kořeny 3 a -4.
A víš, že 
Najdi diferenci a máš hotovo.
3)
Pouze vzorec:
---
A já jdu obědvat, se zbytkem pomůže někdo jiný.
Offline
#3 12. 05. 2009 07:39 — Editoval Cheop (12. 05. 2009 07:46)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Posloupnosti
↑ FinAAAL:
Př.4)
Musí platit:![kopírovat do textarea $\frac{n-1}{2}[30+30+(n-2)(-3)]=8(30+(n-1)(-3))$](/mathtex/f9/f9d875d4f73bd9e98b6016fb75301909.gif) -úpravou dospějeme k rovnici:
-úpravou dospějeme k rovnici: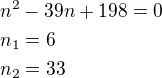
Pro n=6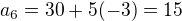
Pro n=33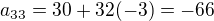
Zkouška:
pro a_6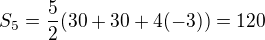
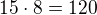
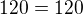
Pro a_33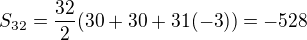
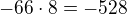
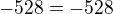
Nikdo není dokonalý
Offline
#4 12. 05. 2009 08:47 — Editoval Cheop (12. 05. 2009 09:09)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Posloupnosti
↑ FinAAAL:
Př.5)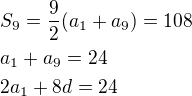
Protože to mají být čísla přirozená, pak: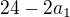 musí být dělitelné číslem 8 což tedy mohou být čísla 24, 16, 8
musí být dělitelné číslem 8 což tedy mohou být čísla 24, 16, 8
a pak:
1) 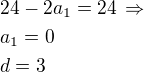
2) 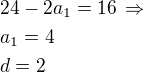
3) 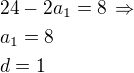
Ta čísla tedy budou:
1) (0,3,6,9,12,15,18,21,24) nebo
2) (4,6,8,10,12,14,16,18,20) nebo
3) (8,9,10,11,12,13,14,15,16)
Poznámka: Nejsem si jist, zda 0 (nula ) patří mezi čísla přirozená.
Nikdo není dokonalý
Offline