Matematické Fórum

↑ stucja01:
Hezký den,
věta v této formulaci neplatí, protože nějaké lineární uspořádání lze vymyslet velmi snadno. Tak například můžeme srovnávat komplexní čísla v exponenciálním tvaru podle absolutní hodnoty a v případě rovnosti podle úhlu v intervalu 0 až 2pi.
Tím zásadním problémem je, že nad tělesem komplexních čísel není možné sestrojit lineární uspořádání, které by doplnilo těleso komplexních čísel na uspořádané těleso.

by bylo uspořádané těleso, pokud by platilo pro všechna a, b a c z C:
1. jestliže 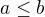, pak
2. jestliže 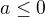a , tak
(pokud se nemýlím, tak se takovému uspořádání říká přirozené uspořádání)

Nejvíce do očí bijící zádrhel bude v chování komplexní jednotky. Když si např. zvolíš a=b=i, budeš to nejspíš pokládat za číslo větší než nula. Ale součin budeš nejspíš pokládat za menší než nula. Takže tohle může být někdy prezentováno jako "jasný důkaz". Ve skutečnosti to je spíše nástin, vlastní důkaz má trochu víc kroků...