Matematické Fórum

vytautas · 13. 06. 2017 15:50

Zdravim

mam problem so 6.
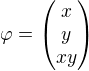Skusal som substituciu $x=r\cos(\alpha)$ , $y=r\sin(\alpha)$ $z=\frac{r^2}{2}\sin(2\alpha)$ ale viedlo to len na zlozity integral, ktory nie som schopny spocitat, podobne pre parametrizaciu $\varphi= \begin{pmatrix}x \\ y \\ xy \end{pmatrix}$ s prislusnymi medzami.

za kazdu radu dakujem.

Jj · 13. 06. 2017 17:40 — Editoval Jj (13. 06. 2017 17:43)

↑ vytautas:

Dobrý den. Řekl bych, že se povrch spočítá integrací

$S = \int_{-1}^{1}\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}\sqrt{1+(z'_x)^2+(z'_y)^2}= \int_{-1}^{1}\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}\sqrt{1+x^2+y^2}\,dy\,dx$

---> po transformaci do cylindrických souřadnic (r, fí, z)

$S=\int_0^{2\pi}\int_0^r r\sqrt{1+r^2}\,dr\,d\varphi = \cdots$

zřejmě s výsledkem podle materiálu v odkazu.

Poznámka: V materiálu je uveden rotační hyperboloid, podle mě jde o hyperbolický paraboloid.

Matematické Fórum

#1 13. 06. 2017 15:50

integral

#2 13. 06. 2017 17:40 — Editoval Jj (13. 06. 2017 17:43)

Re: integral

Zápatí