Matematické Fórum

liamlim · 07. 07. 2017 12:54

Zdravím. Tak se mi po dlouhé době znovu podařilo "dokázat" Velkou Fermatovu větu :D Případnému čtenáři budu vděčný za informaci o nalezené chybě až si jí všimne. Za případnou pomoc předem děkuji.

Nejprve předpoklady, ze kterých se budu snažit vyvodit spor (nejvyšší společný dělitel čísel $k$ , $l$ značím $D(k,l)$ a množinu všech prvočísel 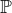$\mathbb{P}$ ):
V1: 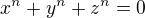$x^n + y^n + z^n = 0$
V2: $xyz \ne 0$
V3: $n\in\mathbb{P}$
V4: $n\ge 7$
V5: $D(x,y) = D(y,z) = D(z,x) = 1$
V6: $x > 0$ , $y > 0$ , $z < 0$

Nyní pomocná tvrzení, která později využiji:
P1: Pro libovolná nesoudělná $k$ , $l$ a prvočíselné $m$ platí, že $D\left(k + l, \frac{k^m+l^m}{k + l}\right)\in \{1, m\}$
DP1: Jsem si celkem jistý, že toto tvrzení platí a důkaz je snadný. Myslím, že jsem jej dokonce dával sem na fórum (nebo vztahy, ze kterých přímo tato věta vyplývá). Každopádně se jedná o zajímavé tvrzení, které ještě využiji.

P2: Pokud $k \equiv 0\mod m$ a $l\equiv 0\mod m$ , pak $D(k,l)\equiv 0\mod m$
DP2: Tvrzení je celkem triviální, jeho platnost jde vidět na první pohled

Nyní samotný "důkaz", kdy z předpokladů V vyvozuji spor. Nejprve definujme $a$ , $b$ jako:
$a = x + y - z$
$b = D(x+y,z)$

Z definice $a$ ihned vyplývá:
$(x+y)^n \equiv z^n \mod a$

Nyní si vyjádřeme $x = a + z - y$ a dosaďme do V1. Dostaneme $(a+z-y)^n + y^n + z^n = 0$ , odkud ihned z binomické věty plyne, že $2z^n\equiv 0\mod a$ . Z toho vyvodíme následující:
- Ze $(x+y)^n \equiv z^n \mod a$ máme $2(x+y)^n\equiv 0\mod a$
- Ze V1 máme $2(x^n + y^n)\equiv 0\mod a$

Aplikací P2 a vzápětí P1 dostaneme $2n(x+y)\equiv 0\mod a$ . Aplikací $x+y\equiv z\mod a$ dostaneme $2nz\equiv 0\mod a$ . Aplikací P2 dostaneme $2nb\equiv 0 \mod a$ , neboť $b$ je nejvyšší společný dělitel $x+y$ a $z$ .

Z V6 a nově odvozeného vztahu přitom platí:
$2nb \ge a = x + y - z \ge x + y \ge b^{n-1}$

Kde poslední nerovnost jde ukázat a v případě zájmu ukáži odvození. Tam si nemyslím, že bych měl chybu, ta bude spíš někde jinde. No důležité je, že z toho plyne $2nb \ge b^{n-1}$ , neboli $2n\ge b^{n-2}$ neboli $(2n)^{\frac{1}{n-2}} \ge b$ . Důležité je, že je $b$ shora omezeno klesající funkcí a že dle V4 je $n$ alespoň 7. Přitom pro $n = 7$ už na $b$ zbývá pouze hodnota 1, což nemůže být, neboť nejvyšší společný dělitel $x + y$ se $z$ je alespoň 2. (To plyne z nerovností $x > 0$ , $y > 0$ )

Xellos · 09. 07. 2017 23:14

"Na kazdy problem existuje pekne, jednoduche, samozrejme chybne riesenie."

Hned na zaciatok sa spytam kolko je $D\left(k + l, \frac{k^m+l^m}{k + l}\right)$ pre $k=1,l=4,m=2$ , teda $D(5,\frac{17}{5})$ .

Matematické Fórum

#1 07. 07. 2017 12:54

vfv

#2 09. 07. 2017 23:14

Re: vfv

Zápatí