Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 12. 07. 2017 15:39
- misaH
- Příspěvky: 13460
Re: Důkaz
↑ vlado_bb:
No - tipujem, že táto dáma študuje na VŠ učiteľskú matematiku...
Offline
#4 12. 07. 2017 17:54
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Re: Důkaz
↑ aniuce:
Asi najčastejší spôsob je uvedomiť si, že delenie sa dá napísať pomocou násobenia a potom použiť dôkaz sporom.
Offline
#7 17. 07. 2017 16:49
- sjaustirni

- Příspěvky: 116
- Škola: AAU
- Pozice: student
- Reputace: 4
Re: Důkaz
sjaustirni napsal(a):
↑ aniuce:
Asi najčastejší spôsob je uvedomiť si, že delenie sa dá napísať pomocou násobenia a potom použiť dôkaz sporom.
Offline
#12 01. 08. 2017 16:10
Re: Důkaz
↑ aniuce:
Ahoj.
Podrobný důkaz ovšem závisí na tom, jakým způsobem je daný číselný obor
spolu s aritmetickými operací a uspořádáním vybudován, což je celkem dost práce.
Také je ovšem možno zavést ten který číselný obor axiomaticky a pak to
bude poněkud jiné ...
Offline
#13 02. 08. 2017 07:24
Re: Důkaz
↑ vlado_bb:
-6 / -2 = x
------------
Rovnice to je, pokud se L = P (leva strana rovna prava)
L = -6 / -2
P = x
L = P
A operace, ktere nad rovnici muzes delat je treba nasobeni obou stran -1. Ve skole jsme napravo dali caru, napsali si tam poznamku, ze nasobime -1 a na dalsim radku to pronasobili.
-6 = -2 * x | *(-1)
L * (-1) = P * (-1)
-6 * (-1) = (-2 * x) * (-1)
Pak je treba si davat pozor na scitani a roznasobit obe cisla.
Ale nevim, jestli to neni slozitejsi pro deti :)
Nektere veci je treba brat proste jako fakt, jakoze se cislo 1 pise 1, cisla 3 5 6 9 jsou si vzhledove podobna a je treba si davat pozor a nesplest to pri cteni :)
Kazdopadne, psat si poznamky, je dobre, moc mi to v matice pomohlo, vzdycky jsem mel za 2. Hodne mi pomahalo psat si postup krok za krokum pri operaci s krivkami (polynomy, kruznice, elipsy, vektory)
Offline
#14 02. 08. 2017 07:43
Re: Důkaz
↑ mracek: Ja len ze ak mame dokazat, za podiel dvoch zapornych cisel je kladne (alebo sucin, co je to iste), tak sotva mozeme pouzit, ze 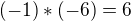 . Preto som sa hned na zaciatku pytal zadavatelky, co je mozne pouzit pri dokaze. Odpoved zatial neprisla.
. Preto som sa hned na zaciatku pytal zadavatelky, co je mozne pouzit pri dokaze. Odpoved zatial neprisla.
Offline
#15 03. 08. 2017 12:15
Re: Důkaz
↑ mracek:
Každopádně je nutné ujasnit si, co o té číselné struktuře již víme (či máme vědět),
Teprve na tomto základě je možno stavět důkaz nějakého dalšího tvrzení.
Co tedy už je Ti známo o číslených operacích a relaci uspořádání ? Napiš to sem a uvidíme.
Viz kolega ↑ vlado_bb:.
Offline
#16 03. 08. 2017 13:36 — Editoval vanok (03. 08. 2017 14:02)
Re: Důkaz
Pozdravujem,
Poznamka.
Na ZS skole sa niekedy pouzival takyto postup. ( pisem schematicky)
Nech x, y su dve kladne cisla.
Vieme, ze (-x) × 0 = 0
Co da: (-x) × ( y – y ) = 0.
A tak: (-x) × y – x × (-y) = 0.
A potom: (-x) × y + (-x)×(-y) = 0.
A potom: (-xy) + (-x)×(-y) = 0.
A na koniec: (-x)×(-y) = xy
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 04. 08. 2017 09:18 — Editoval mracek (04. 08. 2017 09:24)
Re: Důkaz
Tak, pak mne napada, snad jenom pouzit graf (nakreslit), pripadne scitani.
a + a = 2*a
3 + 3 = 6 - souhlas?
-3 + -3 = -6 - souhlas i s timto? pak...
2 * -3 = -6 - a kdyz to podelim -3
2 = -6 / -3
a + a = 2*a
a=+3: 3 + 3 = 6 = 2 * 3
a=-3: -3 + -3 = -6 = 2 * -3
graf
. . . 0
< - o - >
. . . . . 0
< - - - o - - - >
1 carka vlevo (zaporna) 3x, udela 3 carky vlevo
2 carka vpravo 3x udela 3 carky vpravo
A kdyby bylo -3x, tak se prevadi na opackou stranu.
Offline
#20 04. 08. 2017 13:09 — Editoval misaH (04. 08. 2017 13:09) Příspěvek uživatele misaH byl skryt uživatelem misaH.
#22 21. 08. 2017 15:00 — Editoval Rumburak (21. 08. 2017 15:25)
Re: Důkaz
↑ aniuce:
Dk., že podíl dvou kladných čísel je kladné číslo, by mohl vypadat třeba takto (sporem):
Nechť  a předpokládejme, že
a předpokládejme, že 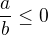 . Existuje tedy
. Existuje tedy 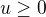
takové, že
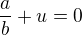 .
.
Když tuto rovnost vynásobíme číslem  , dostaneme
, dostaneme

a dalšími úpravami
 ,
,
(*) 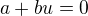 .
.
Avšak čísla 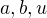 v poslední rovnosti mají splňovat (jak uvedeno výše) podmínky
v poslední rovnosti mají splňovat (jak uvedeno výše) podmínky
 ,
,
takže 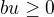 a tedy
a tedy  , čili
, čili  , což je ve sporu s (*).
, což je ve sporu s (*).
Obdobně se zbývajícími důkazy, při čemž lze využít, co už bylo dokázáno dříve.
Offline
