Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 07. 2017 18:40
Weyl-minkowski
Zdravim
mam problem s dokazom / s pochopenim / jednej implikacie Weyl Minkowskeho vety, teda, ze kazdy obmedzeny mnohosten je polytop.
Dokaz je zalozeny na tom, ze mame nas obmedzeny mnohosten  , kde
, kde  su uzavrete polpriestory,
su uzavrete polpriestory, 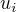 su jednotkove vektory a
su jednotkove vektory a 
Pre  si definujem mnozinu
si definujem mnozinu 
Vyuzivam dalej lemmu(3?), ktora vravi, ze  , kde
, kde  znaci mnozinu extremalnych bodov, teda takych, ktore ked vynechame, neporusi sa konvexita a
znaci mnozinu extremalnych bodov, teda takych, ktore ked vynechame, neporusi sa konvexita a  znaci linearny obal cez
znaci linearny obal cez 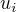 , kde
, kde  .
.
Potom mame pre extremalne body vyjadrenie(1?) :
a z lemmy nakoniec vyplyva(2?), ze  , teda je konecna a z Krein-Milmanovej vety mame, ze
, teda je konecna a z Krein-Milmanovej vety mame, ze  ak
ak  je konvexne teleso, tym padom
je konvexne teleso, tym padom  je konvexnym obalom konecnej mnoziny a teda polytop.
je konvexnym obalom konecnej mnoziny a teda polytop.
Moja otazky: (1?) preco kazdy extremalny bod je prave takeho tvaru ?
(2?) ako to z toho vyplyva ? vobec to nevidim.
(3?) casti dokazu tejto lemmy mi nie su jasne, spisem ich presne neskor, najskor ma zaujimaju (1?),(2?).
za kazdu pomoc dakujem
Per aspera ad astra
Offline

 , proto má soustava jediný řešení (a tím řešením musí být
, proto má soustava jediný řešení (a tím řešením musí být  )
) rovnicemi z
rovnicemi z  možných
možných