Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 25. 06. 2017 19:00 — Editoval vanok (28. 06. 2017 13:24)
Re: Osy, pomery
Ahoj ↑↑ akdar:
Vysledok od Ceva uz sam o sebe zaujimavy vysledok.
Vsak nam da nutnu a postatujucu podmienku aby tri priamky ktore prechadzaju vrcholmi trojuholnika sa pretinali v tom istom bode. ( priamka, ktora prechadza vrcholom trojuholnika sa vola Cevova priamka)
Tento vysledok sa da aj "zlepsit"
Ak urcime jednu orientaciu trojuholnika ABC tri jeho Cevove priamky ktore maju spolocny bod alebo su rovnobezne urcia na stranach tohto trojuholnika usecky ktorych pomer ma sucin -1.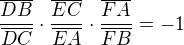
a opacne ak mame pre najake body D, E, F na sranach trojuholnika predosly relaciu, tak AD, BE, CF prechadzaju tym istym bodom alebo su rovnobezne.
Podobne Menelausov vysledok hovori, ze priecka(= priamka ktora pretina strany trojuholnika v bodoch D, C, E) tak 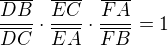
a opacne...
A my mozne vyuzit tieto vysledky na dokaz vety o diagonalach kompletneho stvorstranika.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#77 26. 06. 2017 16:24 — Editoval vanok (26. 06. 2017 20:06)
Re: Osy, pomery
Mala pomoc k jednemu moznemu dokazu vety o diagonalach kompletneho stvorstranika.( pochopitelne aj tie z wikipedii a ine su zaujimave na pre studovanie)
Nakreslil som tento kompletny stvorstranik 
Je mozne pouzit trojuholnik AFE
1)jeho priecka HBD nam da vdaka Menelausovej vlasnosti ....
2)a potom Cevove priamky AG, FD, EB v tomto trojuholniku prechadzaju bodom C, a tak Cevova vlasnost nam da ....
3)delenim prvej a druhej najdenej relacii mame ....
co je jedna charakteristicka vlasnost harmonickeho pomeru, ktoru si ukazala vyssie....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#78 27. 06. 2017 23:58
Re: Osy, pomery
↑ Ahoj vanok:
konečně jsem našla čas se na to pořádně podívat :-)
Jestli jsem to tedy z anglických stránke pochopila správně, tak Menelausův teorem nám říká, že pokud rozdělíme trojúhleník příčkou (jakoukoliv), tak součin poměrů vrchol-průsečík příčky ku průsečík příčky- druhý vrchol na každé straně trojúhelníku nám dá -1
pro tvůj čtyřúhleník tedy plyne:
1) 
dotaz 1: jak je to s orientací úseček, v žádném odkazu nejsou označeny jako vektory, ale podle mě to není jedno, tak teď nevím
Cevauv teorém nám říká, že pokud vrcholy trojúhelníku vedeme přímky, které se protnou v jednom bodě, tak ty nám rozdělí jednotlivé strany a součin poměrů vrchol-dělící bod ku dělící bod - druhý vrchol pro každou stranu nám dá 1.
dotaz 2: takže takovými přímkami jsou například těžnice a výšky?
pro tvůj čtyřúhleník tedy plyne:
2) 
3) podílem tutíž dostaneme: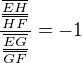
A tady jsem se s dalšími úpravami zasekla (doufala jsem, že vyjde harmonická čtveřice EGFH, ale nevyšla), takže se obávám, že mám někde chybu :-(
Prosím, můžeš na to mrknout :-)
Děkuji a hezký den :-)
Offline
#79 28. 06. 2017 07:53 — Editoval vanok (29. 06. 2017 12:02)
Re: Osy, pomery
Ahoj ↑ akdar:,
Pozor, tu hovorit o stvoruholniku je nepresne, ak sa ti nepaci povedat kompletny stvorstranik, tak pouzi vzdy quadrilatère complet
( stvoruholnik je dany 4mi bodmy, no vsak quadrilatère complet = kompletny stvorstranik je dany 4mi priamkami, ktore sa pretinaju dve po dvoch.... ako som to popisal podrobne vyssie !)
Vlasnosti od Ceva a Menelaus som pripomenul bez dokazu, asi y bolo ich zaujimave tiez dokazat (asi sa velmi uz teraz neucia ... no urobime to neskor, ked skoncime nasu prechadzku harmonickymi stvoricami)
Tvoja poznamka, ze specialne pripady ako taznice trojuholnika ( a ine) su specialne pripady ktore sa daju studovat v pripade vlastnosti od Ceva ... je vyborna. ( a mozes ju pouzit v tychto situaciach).
Tvoj maly problem je len v tom, ze pises trochu inac vlasnosti od Menelaus a Ceva ako som ti to navrhol.... I ked ide o tu istu relaciu v materialoch ktore si pouzila. Jedinny rozdiel je v poradi bodov v danych relaciach: no iste je ti jasne, ze napriklad is 
( pojem pomeru orientovanych useciek, sa sa pozit len ked ide o usecky tej istej priamky....a to nie je vhodne generalizovat na vektory).
Takto, ak pouzijes vlasnosti od Menelaus a Ceva, tak ako som ich pripomenul delenim okazite dostanes dvojpomer  ktory je ten isty ako si nasla ( po malej uprave) a znamena, ze
ktory je ten isty ako si nasla ( po malej uprave) a znamena, ze 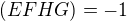 co znamena, ze body H a G delia harmonicky diagonalu EF
co znamena, ze body H a G delia harmonicky diagonalu EF
a tak zväzok  je harmonicky.... co umozni bez vypoctov mat vysledok aj pre ostatne dve diagonaly.
je harmonicky.... co umozni bez vypoctov mat vysledok aj pre ostatne dve diagonaly.
Pred pokracovanim si toto ujasni ( otazky a diskusia je vitana) a potom si pohovorime nieco o Newton-ovej priamke.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#80 11. 07. 2017 23:33
Re: Osy, pomery
↑ Moc zdravím vanok:
právě jsem znovu pročítala ten teorem od Ceva a teď mi spadly z očí šupiny :-) - asi mi to konečně došla ta úplně základní myšlenka - že tři úsečky puštěné z vrcholů se protnou pokud  (bráno z tvého odkazu) - teď jsem si s tím asi půl hodiny hrála v geogebře s posuvníkama a počítala poměry a fakt to vychází :-D To je úžasné, nikdy mě nenapdlo, že se např. těžnice protnou tehdy a jen tehdy pokud je poměr stran a dělících bodů v nějakém vztahu. To je prostě dobrá blbost :-) Pokud budu znát, kde mi protnou 2 výšky jejich strany, dopočítám, kde protne třetí výška třetí stranu :-) I když tahle se to asi nepoužívá.
(bráno z tvého odkazu) - teď jsem si s tím asi půl hodiny hrála v geogebře s posuvníkama a počítala poměry a fakt to vychází :-D To je úžasné, nikdy mě nenapdlo, že se např. těžnice protnou tehdy a jen tehdy pokud je poměr stran a dělících bodů v nějakém vztahu. To je prostě dobrá blbost :-) Pokud budu znát, kde mi protnou 2 výšky jejich strany, dopočítám, kde protne třetí výška třetí stranu :-) I když tahle se to asi nepoužívá.
Jinak co se týče komletnního stvorstanik a čtyřúhleníku, tak chápu rozdíl, jen jsem nenašla v češtině překlad, budu tedy používat komplený stvorstranik.
Děkuji za vyjasnění poměru orientovaných úseček, už v tom mám jasno a doupravila jsem můj 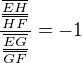 na
na 
chápu že, svazek  je harmonický, ale netušim, co myslíš větou: co umozni bez vypoctov mat vysledok aj pre ostatne dve diagonaly (vycházím z Tvého obrázku z 26.6.), můžeš mi to prosím upřesnit.
je harmonický, ale netušim, co myslíš větou: co umozni bez vypoctov mat vysledok aj pre ostatne dve diagonaly (vycházím z Tvého obrázku z 26.6.), můžeš mi to prosím upřesnit.
Děkuju a přeji hezký den :-)
Offline
#81 12. 07. 2017 14:08 — Editoval vanok (12. 07. 2017 14:11)
Re: Osy, pomery
Ahoj ↑ akdar:,
Vidim, ze sa ti tato klasicka ( a uz skoro zabudnuta) gemetria ozaj paci.
Ked som pisal " bez vypoctov " myslel som na vyuzitie vlasnosti zväzkov.
Tak napr. zväzky (A, EFHG) a (A,DBHI) su totozne a preto priecky EFHG a DBHI maju ten isty dvojpomer, (ten je -1) a su sucasne harmonicke
A pre tretiu diagonalu pozri zväzok (E, DBHI) ....to lahko dokocncis, ze.....
Teraz mozes skusit dokazat (Newton-ova veta)
stredy diagonal kompletneho stvorstanika su na jednej priamke
Pouzi obr. v #77, kde diagonaly su usecky AC, BD, EF.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#82 13. 07. 2017 23:25
Re: Osy, pomery
↑ Ahoj vanok:
Tak pro třetí diagonálu mám (E, DBHI) a (E, AICG) :-)
A teď se chci zeptat, mám chaos v tom, co jsou diagonály - v odkaze #71, to jsou jiné než které označuješ na obrázku #77, ačkoliv u obou máš, že diagonály jsou AC, BD a EF.
Jde o tom, že pro obrázek v #77 mi prostě nevychází, že středy jsou na přímce :-( - diagonály jsou červeně
pokud použiji značení toho, co jsou diagonály z #71, tak to vyjde
(ani tak nemůžu přijít na ten důkaz :-) - už nad sedím asi hodinu, asi budu pokračovat zase zítra, tak bych chtěla mít jistotu, že to mám dobře nakreslené
Hezký den :-)
Offline
#83 14. 07. 2017 00:27
Re: Osy, pomery
↑ akdar:
Pozdravujem.
Aj na prvom obrazku je to dobre. ... len ten stred S3 je spatne urceny.
Zajtra ti dam navrh na jeden mozny dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#87 14. 07. 2017 15:27 — Editoval vanok (17. 07. 2017 01:06)
Re: Osy, pomery
↑ akdar:,
Pozdravujem, myslienka je : pouzit Menelaus-ovu vlasnost.
Cez S1, ved ronobezku z AB,( cez S2 rovnobezku z CD; cez S3 rovnobezku z BC) . Tieto rovnobezky urcia v trojuholniku CBF body X,Y,Z ktore ktore su stredy jeho stran.
To znamena, ze ak plati Menelausova vlasnost v trojuholniku XYZ..... tak body S1,S2,S3 su na jednej priamke.
Staci? Alebo mam pokracovat?
( pozri prvy obrazok z #82)
Poznamka. Tvoj druhy obrazok v #82 neukazuje len diagonaly, ale aj predlzenia stran daneho stvorstranika....
Edit. Oprava preklepu... trojuholnik CBF.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#88 16. 07. 2017 18:53 — Editoval vanok (16. 07. 2017 18:56)
Re: Osy, pomery
Pokracovanie.
Menelaus_ovu vlasnost, ktoru treba dokazat :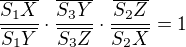 (*)
(*)
No vsak 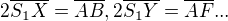
Co po nasobeni vsetkych clenov v (*) cislom 2 nam da ekvivalentne ....
No posledna relacia je evidentne platna ( pozri konstrukciu na pouzitom obrazku), vdaka Menelaus-ovej vlasnosti v trojuholniku. .... pre jeho priecku .....
Na pokracovanie......
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#89 16. 07. 2017 21:49 — Editoval akdar (17. 07. 2017 23:43)
Re: Osy, pomery
↑ Zdravím vanok:
až teď jsem se k tomu dostala a někde jsem zřejmě udělala chybu:
udělala jsem obrázek - rovnoběžky ze středů (zelené)
a pokud ho mám dobře (píšeš, že X,Y,Z jsou středy (edit:) stran trojúhleníku EBF, ale mě vyšel CBF), tak mě zarazilo, že by Menelaus_ova vlastnost měla platit i pro přímku která ten trojúhleník neprotíná(žlutá - spojující středy, což chceme dokázat), to by mě nenapadlo, ale z Tvého pokračování mi to vyplynulo - takže jak jsi vzal (*) chápu, ale vůbec nerozumím, kde jsi vzal 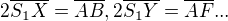 a nedokážu pokračovat pro další strany
a nedokážu pokračovat pro další strany
předpokládám, že mám tedy někde chybu :-(
Offline
#90 16. 07. 2017 23:51 — Editoval misaH (17. 07. 2017 00:00)
- misaH
- Příspěvky: 13459
Re: Osy, pomery
↑ akdar:
Ahoj.
Druhá odmocnina z 1 nemôže byť -1.
Síce platí, že 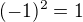 , ale druhá odmocnina podľa definície je také n e z á p o r n é číslo, pre ktoré platí...
, ale druhá odmocnina podľa definície je také n e z á p o r n é číslo, pre ktoré platí...
Rovnako (v SŠ matematike) sa za základ odmocnín berie vždy len nezáporné číslo
Toto sú všetko veci o dohodách (definíciách)...
A ešte:
Síce už dávno nesledujem tie vaše debaty o trojuholníkoch, ale občas niektorý text očami prejdem. Stred trojuholníka neexistuje. Alebo áno?
Offline
#91 17. 07. 2017 01:13 — Editoval vanok (17. 07. 2017 01:14)
Re: Osy, pomery
Doplnim ( nie teraz, ale coskoro) uplne dokaz. A potom si ho podrobne prestudujes.
↑ misaH:
Co sa tyka stredu trojuholnika, tak nikde som stred trojuholnika nedefinoval ( i ked u niektorych autoroch najdeme te to pojem ako stred opisanej kruznice), ale ak si citala moj predosly prispevok, tak si mohla poznamenat, ze X,Y,Z su stredy stran v trojuholniku CDF.
↑ akdar:
Teraz poznamenam, len ze skutocne ide o trojuholnik CDF, ako si to spravne poznamenala.
Co sa tyka odmocnin kolegina Misa urobila spravnu poznamku.
Priecka trojuholnika pretina priamky trojuholnika, a to neznamena, ze to musia byt vnutorne body jeho stran.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#93 17. 07. 2017 15:52
Re: Osy, pomery
Ahoj ↑ akdar:,
Jednu vec som dost nepresnil, body Y a Z treba prehodit na tvojom nacrte #89.
Potom uvidis vdaka podrobnosti trojuholnikov ze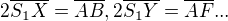
Prva rovnost sa vidi pretoze ABC a  su podobne
su podobne
Druha z podobnosti AFC a  ( pozor na obrazku prehod Y a Z)
( pozor na obrazku prehod Y a Z)
Ine rovnosti na dokaz su
Tie dve posledne najdes?
Po uprave co som popisal v #88 5ty riadok dostanes vdaka najdenym rovnostiam relaciu .... ktora plati lebo, podla konstrukcii jasne ze priecka E,D, A (tie body su na tej istej priamke) je priecka trojuholnika CBF.
Dokazes teraz, ten dokaz ukoncit?
Poznamka ( doplnok).
Priecka jedneho trojuholnika moze pretnut len :
dve strany v ich vnutry, alebo
ziadnu ( cize vsetki tri priamky stran pretinaju priecku mimo ich vnutornych useciek).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#95 17. 07. 2017 23:42
Re: Osy, pomery
↑ Ahoj misaH:
děkuji za odpověď. Právě, že mě nikdy ani nenapadlo, že by  , jenže mě přišly všechny ty úpravy správné, ale nesedí mi, že pak vyjde -1 = 1. Tak jsem jen chtěla vědět, kde je chyba.
, jenže mě přišly všechny ty úpravy správné, ale nesedí mi, že pak vyjde -1 = 1. Tak jsem jen chtěla vědět, kde je chyba.
A děkuji za upozornění na střed trojúhleníka, jdu to opravit :-)
Offline
#96 17. 07. 2017 23:50 — Editoval akdar (17. 07. 2017 23:51)
Re: Osy, pomery
↑ Ahoj vanok:
teď už je mi to jasné,
vyjde  ,
,
což (jak píšeš) platí, protože je to příčka.
Offline
#97 18. 07. 2017 00:39 — Editoval vanok (18. 07. 2017 01:11)
Re: Osy, pomery
↑ akdar:
Pozdravujem, vidim, ze napredujes.
Teraz, ako zaujimave cvicenie je popisat konstrukciu: nech su dane body A,B,C na jednej priamke, construire bod D, taky aby stvorica (ABCD) bola harmonicka.
Ako dalsiu temu co vyuzije a prehlbi tvoje poznatky, by bolo dobre vidiet pojem polu a polarity. To nam zobere trochu casu. Ale to je prijemne napredovat, ze.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#98 20. 07. 2017 00:17
Re: Osy, pomery
Ahoj vanok,
využiji tvzení z #69:
vanok napsal(a):
Nutna a postatujuca podmienka aby jeden zväzok 4roch polopriamok ( lucov) spolocneho pociatku bol harmonicky je aby jedna rovnobezka z jednym jeho lucov bola rozdelena na dve rovnake usecky tromi inymi lucmi.

z libovolného bodu (H) vedu polopřímky přes A,B,C
např. v B vedu rovnoběžku s AH
v místě kde rovnoběžka protne polopřímku HC je střed úsečky E
přenesu vzdálenost BE - dostanu bod G, kterým musí procházet čtvrtá polopřímka
udělám polopřímku HG a kde se protne s přímkou, na které leží A,B,C je hledaný bod D
Je to dobře?
A co se týká dalších informací, já bych se moc ráda dostala k počátečnímu tématu - Apollóniova kružnice :-)
Offline
#99 29. 07. 2017 00:19
Re: Osy, pomery
↑ Zdravím vanok:
k polům a polaritě jsem našla toto: https://www.pf.jcu.cz/stru/katedry/m/MRG/apollo.pdf - str. 15
Offline
#100 30. 07. 2017 13:17
Re: Osy, pomery
Ahoj ↑ akdar:,
Vidim, ze si studovala aj ine materialy pokial som trochu dovolenkoval.
Teraz sme v stadiu, ze mozme otvorit nove vlakno typajuce sa Apollonius-ovych kruznic tykajucych sa trojuholnika. To urobime tak, ze najprv pripomenieme vsetki vlasnosnosti co sme uz ( prakticky) dokazali a potom este pojdem trosku dalej a pokusime sa dokazat aspon niekolko dalsych....
Co sa tyka polov a polarity, je prirodzene pokracovat v tomto vlakne ( ako stredoskolaci v 20-tom storoci)!
Tak niekolko definicii. ( obrazky ku kazdej definicii, necham na teba)
Definicia.
Dva body P a M su harmonicky konjugovane relativne k pretinajucym sa priamkam OA a OB, ak harmonocky delia usecku DC, kde C a D su body prieseku priamky PM z priamkamy OA a OB .
Ak bod M je harmonicky konjugovany z bodom P relativne k priamkam OA a OB,
potom priamka OM sa vola polara bodu P
a bod sa vola P pol priamky OM relativne k OA a OB ( alebo aj k uhlu AOB)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



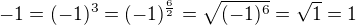
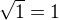 , že je to vlastně jen dohoda, že by to mohlo být klidně
, že je to vlastně jen dohoda, že by to mohlo být klidně 