Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 10. 2017 13:23 — Editoval wq (03. 10. 2017 13:44)
Dělení nulou
Dobrý den,
Ze všech stran slyším, že jmenovatel nesmí být nula. Nejčastější argument je, že kdyby 1/0=a (místo jedničky by tam mohlo být jakékoliv nenulové číslo), pak a*0=1, což nejde, protože cokoliv*nula je nula. Ale co kdyby jsem napsal místo jedničky nulu, tj. 0/0=a. Pak by a*0=0, což nejenže není nesmysl, ale dokonce platí pro všechna čísla a. Takže 0/0=0, 0/0=50, 0/0=-1…atd. Samozřejmě nechci tvrdit, že 0=50=-1, ale jen to, že 0/0 má nekonečno řešení a ne naopak žádné, jako je tomu v případě nenulového čísla v čitateli. Přestože nedokážeme určit přesnou hodnotu tohoto výrazu, není to nesmysl a není tedy třeba např. k výrazu a/a psát, že a≠0. Prosím napište svůj názor a podepřete ho nějakými argumenty. Děkuji
PS. Další věc je dvojí řešení rovnice 2x=x
x=2x / -2x
-x=0 / .(-1)
x=0
x=2x / :x
1=2
x/x=0:0=1
2x/x=0:0=2
Offline
#3 03. 10. 2017 13:39
Re: Dělení nulou
↑ vlado_bb:
Za normálních okolností ano. Vlastně určitě ano.
Proto taky nemůžeme 0/0 konkrétně spočítat, ta hodnota prostě závisí na okolnostech. Teď jsem si třeba vzpomenul na jeden ze Zénónových paradoxů, o letícím šípu. V nulovém čase urazil nulovou dráhu, takže rychlost je 0/0. Z toho nezjistíme jestli letí například 10m/s nebo15m/s, ale pochopitelně ne obojí najednou.
Offline
#4 03. 10. 2017 13:44
Re: Dělení nulou
wq napsal(a):
↑ vlado_bb:
Vlastně určitě ano.
Tento argumnet uplne staci, nie je potrebne angazovat Zenona. Nemoze byt sucasne  a tiez
a tiez  .
.
Offline
#5 03. 10. 2017 13:49
Re: Dělení nulou
↑ vlado_bb:
Omlouvám se, nevyjádřil jsem se přesně. Ve skutečnosti neplatí, že 0/0=1 a zároveň 0/0=2. Chtěl jsem říct, že nemůžeme vědět, zda se 0/0=1, NEBO 0/0=2, nebo cokoliv jiného.
Offline
#9 03. 10. 2017 14:09
Re: Dělení nulou
↑ vlado_bb:
Sám o sobě sice neoznačuje žádné konkrétní číslo, ale za určitých podmínek může označovat jakékoliv reálné (a vlastně asi i nereálné) číslo.
Offline
#11 03. 10. 2017 14:30
Re: Dělení nulou
↑ vlado_bb:
A co nekonečno - vždyť taky neoznačuje žádné reálné číslo a přesto nikdo nezpochybňuje jeho existenci.
A co se týče nekonečna a pravidla a=b a=c b=c, je to podobné jako 0/0.
b= a=b+1=
a=b+1= a přesto a≠b.
a přesto a≠b.
Offline
#12 03. 10. 2017 14:44 — Editoval vlado_bb (03. 10. 2017 14:45)
Re: Dělení nulou
↑ wq:  ale nie je cislo, ale symbol, takze zapis
ale nie je cislo, ale symbol, takze zapis  je nezmyselny. Pokial teda nehovorime o kardinalitach, potom ale uplne iny vyznam ma ako
je nezmyselny. Pokial teda nehovorime o kardinalitach, potom ale uplne iny vyznam ma ako  , tak
, tak 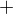 . A ano, nikto nespochybnuje existenciu nekonecnych mnozin, ale rovnako ani nikto netvrdi, ze existuje nejake nekonecne realne cislo.
. A ano, nikto nespochybnuje existenciu nekonecnych mnozin, ale rovnako ani nikto netvrdi, ze existuje nejake nekonecne realne cislo.
Offline
#13 03. 10. 2017 15:03
Re: Dělení nulou
↑ vlado_bb:
No,  jsem měl na mysli tohle:
jsem měl na mysli tohle:
Představte si množinu A o nekonečnu prvcích a množinu B, která zahrnuje A a ještě jeden prvek navíc. Přestože obě mají nekonečno prvků, neznamená to, že jsou stejně obsáhlé.
Ale dobře, asi máte pravdu, já se v nekonečnu zase tolik nevyznám.
Vraťme se tedy k té nule - pořád jste nic neřekl například na ten letící šíp, který má v okamžiku rychlost 0/0.
Zatím téma nechci uzavírat, třeba se k němu vyjádří ještě někdo další.
Offline
#14 03. 10. 2017 15:12
Re: Dělení nulou
wq napsal(a):
↑ vlado_bb:
pořád jste nic neřekl například na ten letící šíp, který má v okamžiku rychlost 0/0.
Nema rychlost  , ale
, ale  , kde
, kde 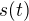 je draha v case
je draha v case  .
.
Offline

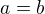 a sucasne
a sucasne  , tak
, tak  ?
? .
.