Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kombinatorika - Princip inkluze a exkluze př.
#1 07. 10. 2013 14:40
Kombinatorika - Princip inkluze a exkluze př.
Zdravím,
můžete mi prosím pomoc jak se do tohoto příkladu zakousnout nějak mi to furt nesepína.
Na účtu v restauraci je zapsáno pět položek: čaj, kofola, pivo, rum, fernet. Kolika způsoby se mohou o zaplacení podělit tři hosté, má-li každý zaplatit alespoň jeden nápoj?
Offline
- (téma jako nevyřešené označil(a) Fires)
#2 07. 10. 2013 15:46
Re: Kombinatorika - Princip inkluze a exkluze př.
↑ Fires:
Ahoj,
představ si to vizuálně - tam, kde máš v seznamu čárky nebo tečku, chceš umístit jednoho hosta. Použiješ interpretaci, že každý host platí vše, co je vlevo od něj až dokud nenarazí na konec seznamu nebo na dalšího hosta. Pokud v tom vidíš, že takhle je zaručeno, že každý platí alespoň jeden nápoj, je to už jen o dosazení do příslušného kombinatorického vzorce:-)
Доктор сказал «в морг» — значит в морг!
Offline
#3 07. 10. 2013 16:01
Re: Kombinatorika - Princip inkluze a exkluze př.
↑ Fires:
Pro zaplacení čaje máš 3 možnosti, pro zaplacení kofoly taktéž atd.
To znamená, že všech možných způsobů zaplacení je 
Jenže v tom jsou i možnosti, že jeden nepaltil. Těch je 
Jenže v tom jsou i možnosti, že dva neplatili, ty jsou  , a ty jsme v předcházející variantě započítali dvakrát, takže je musíme odečíst
, a ty jsme v předcházející variantě započítali dvakrát, takže je musíme odečíst
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 07. 10. 2013 20:47
Re: Kombinatorika - Princip inkluze a exkluze př.
Tak ten priklad jsem pochopil ale asi ne z jeho podstaty. Druha varianta prikladu:
{caj,kofola,pivo,rum,fernet,vodka} -> 6 nápoju
5 hostů
Každý musí zaplatit alespon jeden napoj.
Tak by mělo byt: = celkovy pocet moznosti
= celkovy pocet moznosti
Varianta ze jeden nezaplati (jedina varianta kdy nekdo neplati, protoze 6 napoju a 5 lidi )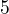
tzn. výsledek má být ale
výsledek má být ale 
Offline
#7 18. 10. 2013 13:05
Re: Kombinatorika - Princip inkluze a exkluze př.
Domki napsal(a):
Taky řeším tento příklad.
Ale chápu jen to kde vemeš toto: To znamená, že všech možných způsobů zaplacení je.
Ale to dál nějak nechápu co to má znamenat a kde to vemu? Jako podle čeho?
Najde se někdo kdo by mohl zodpovědět a vysvětlit postup řešení tohoto příkladu nějak podrobněji, stále tomu nemohu nějak přijít na kloub.
Offline
#8 07. 10. 2017 14:33 — Editoval Bas (07. 10. 2017 14:39)
Re: Kombinatorika - Princip inkluze a exkluze př.
Nšel sem to až teď, ale co kdyby se ještě nekdo zajímal...
zdenek1 napsal(a):
jedná se o tzv princip inkluze a exkluze (tedy součet množin) kdy musíme střídavě odečítat a sčítat průniky většího počtu množin:
S = všechny možnosti, pro n hostů při m položkách je to  , protože každá položka může být zaplacena n způsoby
, protože každá položka může být zaplacena n způsoby
A, B, C, D.... = množiny všech možností, kdy 1 člověk nezaplatí (počet množin = počet lidí logicky) = 
AB, AC, AD, BC, BD, CD ... = průniky právě dvou množin, kdy zaráz 2 lidé nezaplatí = 
a pak už jen potřebujeme sečíst všechny množiny A - X, kde budeme dělat průnik a dostaneme počet možností, kdy nezaplatí jeden nebo druhý... až nebo x-tý, tedy kdy NĚKDO nezaplatí
no a VŠE mínus NĚKDO nezaplatí = každý zaplatí (alespoň jednu položku)
proto je výše použita kombinace pro určení počtu průniků:
kolik mám průniků množin A, B, C?:
1) 2: AB, AC, BC (3x)
2) 3: ABC (1x)
nebo zkusím udělat 2/3 skupiny ze 3 prvků:
1) 2:  nebo taky
nebo taky  (3x)
(3x)
2) 3: 
tzn pro třeba 7 čajů a 4 lidi:
a tohle odečtu od celkového počtu možností (proč nula na sedmou? průnik všech 4 množin je přece že nikdo nezaplatí, což ale nenastane, protože někdo to zaplatit musí, tedy alespoň jeden platí vše)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kombinatorika - Princip inkluze a exkluze př.


