Matematické Fórum

Zvedavec 4 · 09. 10. 2017 16:01

Docetl jsem se, ze jednim z dukazu Teorie Relativity by bylo to, ze miony, ktere jsou utvoreny nejakych 20km nad zemi, a ktere se rozpadaji behem 2 mikrovterin dorazi az na zem prave kvuli efektum TR. Pri predpokladany rychlosti 99.99% c, tedy nejakych 299 970km/s, kdy gama = 71 se totiz "doziji" 14 milivterin a tudiz pri te rychlosti a za tu dobu jsou schopny doletnout 42 km a tim je vysvetlena zahada toho, ze jsou pozorovany na zemi anebo dokonce hluboko pod zemni v jeskynich. Jinak by pri jejich zivotnosti a stejne rychlosti mohly doletnout jenom 600 m. Tedy, ze ve vztazne soustave pozorovatele na zemi by pricinou vysledku byla dilatace casu samotna.

Pak ten clanek pokracuje tim, ze ve vztazne soustave toho mionu ale cas bezi normalne, ale je to vzdalenost ve smeru jeho letu, co se smrskne 71x a tudiz se dosahne stejneho vysledku, tedy ze muze doletet az na zem nez se rozpadne. Tedy, ze ve vztaznee soustave toho mionu by pricinou vysledku byla kontrakce delek samotna.

Tenhle a podobne priklady se zdaji potvrzovat nahled, ze dilatace casu a kontrakce delek jsou dve strany jedne mince, tedy, ze bud jedna nebo ta druha budou pricinou treba toho, ceho jsem se docet na jine seriozni webove strance, a to ze se da dosahnout treba souhvezdi Andromedy, vzdalenem 2 000 000 sv.let za 40 let kosmonautova zivota, kdy tedy gama by musela byt nejakych 50 000 a tedy rychlost rakety 299,999.999 939 999 999 993 999 999 998 8 km/s.

Jina seriozni webova stranka ale pri vysvetlovani dilatace casu pomoci svetelnych hodin ukazuje, ze pri hodinach nasmerovanych kolmo vuci smeru letu rychlosti 0.995c, tedy 298 500km/s, bude gama=10, ale nasmerujeme-li je po smeru letu, gama bude 100. Jiste je tenhle priklad znamy a nemusim zachazet do detajlu. Ale co je dulezite je to, ze tenhle priklad se zda jasne ukazovat, ze oboji, jak dilatace casu tak i kontrakce delek pusobi kombinovane a tudiz by gama v priklade s Andromedou byla pouhych 224 a rychlost by stacila byt "pouhych" 299 997 km/s.

Ten druhy prapad se me osobne zda byt mnohem vic prijatelnym.

Existuje tedy jasna odpoved na tenhle zdanlivy rozpor?

LukasM · 09. 10. 2017 16:41

↑ Zvedavec 4:
A nemohl by sis dát tu práci a dát sem odkazy na všechny zmiňované seriózní webové stránky? Pak by bylo jasnější, o čem mluvíš.

Zvedavec 4 · 09. 10. 2017 17:22

Promin, nechtel jsem tim zatezovat a jsou navic Anglicky, a taky vidim, ze vetsinou jste vsichni v STR a hlavne v matematice mnohem vic znali nez ja. Ale tady jsou:

"Einstein for Everyone" John D. Norton; dalsi jsou z Wiki o "STR" a ta treti je z Massachusetts Institute of Technology Department of Physics
"Lecture 11: Spacetime: Introduction to Special Relativity".

LukasM · 09. 10. 2017 18:26 — Editoval LukasM (09. 10. 2017 18:29)

↑ Zvedavec 4:
Jak vidím ten mion:

1.Mion ze svého pohledu žije dejme tomu přesně 2 us, vzdálenost k Zemi vidí kontrahovanou, a proto ji stihne uletět. Dochází tedy ke kontrakci délek, protože z pohledu stojícího mionu (!!!) je kontrahovaná letící Země a vzdálenost k ní. Současně dochází k dilataci času, protože z pohledu mionu na hodinách pozorovatele na Zemi ubíhá čas rychleji, než jak ubíhá mionu. To ovšem mion nemá moc jak zjistit.

2. Soustava pozorovatele na Zemi: jsem v klidu, mion se vůči mně pohybuje rychle a dochází k dilataci času, protože z mého pohledu (!!!) mionu běží hodiny pomaleji než mně - proto se můžu divit, jaktože mion ještě žije. Současně dochází ke kontrakci délek, kdyby mion letěl v nějaké krabici (která se pohybuje s ním), jevila by se zkrácená. Ovšem nic takového tam není, takže kontrakci není na čem pozorovat.

A teď ty kolmé světelné hodiny. Dejme tomu, že mám v lodi kolmo k sobě dvoje stejné světelné hodiny - jedny podélně a druhé příčně ke směru pohybu lodi. Vzdálenost mezi zrcadly je v klidové soustavě v obou případech stejná. Stejné hodiny mám na Zemi.

1. Při pohledu z lodi je vše v pořádku. Oboje hodiny tikají stejně.

2.
a) Při pohledu ze Země jdou příčné hodiny pomaleji než hodiny na Zemi, protože světelný paprsek v těch letících urazí delší dráhu. Jdou přesně $\gamma$ -krát pomaleji, což plyne z elementární geometrie. Tomuto jevu se říká dilatace času. Z pohledu pozorovatele na Zemi je loď podélně zkrácená, ale na hodiny to nemá žádný vliv (kromě toho, že vypadají směšně).

b) Při pohledu ze Země jdou podélné hodiny pomaleji ze dvou důvodů. Jednak zrcadlo vždy letí světlu naproti, nebo se mu snaží uletět (nevyruší se to, zamysli se proč), jednak je loď podélně zkrácená a zrcadla se nám zdají blíž k sobě. První vliv způsobí zpomalení hodin faktorem 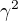$\gamma ^2$ (opět elementární výpočet). Druhý vliv je zrychlí faktorem $\gamma$ . Ve výsledku jdou tedy opět $\gamma$ -krát pomaleji, než hodiny na Zemi. Což je nutné, jinak by se z pohledu Země hodiny na lodi vůči sobě rozcházely, což není možné. Došlo tedy ke kontrakci délek. Kdyby vedle hodin chodil kosmonaut a ukazoval na nás neslušná gesta, viděli bychom to zpomaleně. To na chod hodin ovšem nemá žádný vliv.

To, co mi ve tvém příspěvku připadá nesprávné je tvrzení "pri hodinach nasmerovanych kolmo vuci smeru letu rychlosti 0.995c, tedy 298 500km/s, bude gama=10, ale nasmerujeme-li je po smeru letu, gama bude 100", a také jsem ho nikde v odkazovaných materiálech nenašel.

Zvedavec 4 · 10. 10. 2017 02:34

Lukas Napsal

b) Při pohledu ze Země jdou podélné hodiny pomaleji ze dvou důvodů. Jednak zrcadlo vždy letí světlu naproti, nebo se mu snaží uletět (nevyruší se to, zamysli se proč), jednak je loď podélně zkrácená a zrcadla se nám zdají blíž k sobě. První vliv způsobí zpomalení hodin faktorem $\gamma ^2$ (opět elementární výpočet). Druhý vliv je zrychlí faktorem $\gamma$ . Ve výsledku jdou tedy opět $\gamma$ -krát pomaleji, než hodiny na Zemi. Což je nutné, jinak by se z pohledu Země hodiny na lodi vůči sobě rozcházely, což není možné. Došlo tedy ke kontrakci délek. Kdyby vedle hodin chodil kosmonaut a ukazoval na nás neslušná gesta, viděli bychom to zpomaleně. To na chod hodin ovšem nemá žádný vliv.

Lukasi, dekuju za odpoved.

Jak to pracuje celkem chapu. Ale neznamena todle, ze ty dva efekty, dilatace a kontrakce, pusobi oba soucasne, tedy ze se nasobi, bez ohledu na soustavu, ze ktere se to zvazuje, a proto je vysledkem ta $\Gamma ^{2}$ ?

Ze oboji ty hodiny, tedy pricny a podelny, musi ukazovat stejny cas je mi jasny. Ta $\Gamma$ , ktera vznika diky zkraceni podelnych hodin, a ktera ten jejich chod naopak zrychli s celkovym vysledkem, ze budou ukazovat stejne jako ty pricny, tedy celkove jenom $\Gamma$ -krat pomalejs nez hodiny v "nehybne soustave" na Zemi, a ktera ma vliv jenom na vysledny chod hodin, neni tedy zaroven dukazem, ze tomu tak je, tedy ze se ty dva efekty nasobi, tedy ze se $\Gamma$ umocnuje prave na 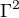$\Gamma^{2}$ diky "dilataci vynasobene kontrakci"?

A tedy to, ze tudiz v priklade s Andromedou (cisla, krome tech 40 let zivota kosmonauta, jsem dosadil ja [to v pripade, ze tam je chyba]) bude stacit dosahnout tu rychlost druhou, tedy pomalejsi s gamou co se rovna 224 aby se tam raketa dostala za tech pouhych 40let kosmonautova zivota? Tot ma otazka, protoze ten priklad s mionem se zda tvrdit pravy opak.

Zvedavec 4 · 10. 10. 2017 02:40

To, co mi ve tvém příspěvku připadá nesprávné je tvrzení "pri hodinach nasmerovanych kolmo vuci smeru letu rychlosti 0.995c, tedy 298 500km/s, bude gama=10, ale nasmerujeme-li je po smeru letu, gama bude 100", a také jsem ho nikde v odkazovaných materiálech nenašel.

Tohle je v prispevku "Einstein for Everyone" Johna D. Nortona, kde on tam udava takovy vysledek a prave si myslim, ze chce rict, ze vysledna $\Gamma$ se prave umocnuje. Jediny, co bych mohl, by bylo to sem okopirovat.

Zvedavec 4 · 10. 10. 2017 12:21

Je dost mozny, ze i v tom priklade s mionama je todleto mysleny, ale v tom pripade by se to zdalo tedy byt nepresne vyjadreny, protoze to dava dojem, ze z hlediska pozorovatele na zemi by cely prepocet gama=71 byl zpusobeny dilataci samotnou a z hlediska mionu by byl zpusobenej kontrakci vzdalenosti samotnou.

Kdyz si ale vezmu uvahu s hodinama coby spravny zaklad, a vypada to, ze presne takova by byla mohla byt puvodni Einsteinova uvaha, protoze v ni jsou obsazeny vsechny zakladni principy TR, rek bych, ze jak dilatace tak kontrakce samy o sobe muzou byt jenom pricinou 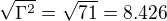$\sqrt{\Gamma^{2} }=\sqrt{71}=8.426$ a tedy $\Gamma$ =8.426 a tudiz by stacilo aby ten mion letel rychlosti v=297 879.8321km/s a ne jak se v priklade tvrdi 299 970km/s.

To samy v priklade s Andromedou by cast gamy byla zpusobena dilataci a ciselne tou samou gamou zkracena vzdalenost k ni kontrakci, takze 224x224=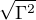 $\sqrt{\Gamma^{2} }$ =50 000.

Doufal jsem, ze to nekdo bud potvrdi anebo vyvrati. Asi si je tezko v techhle popisech rozumnet tudiz je celkem mozny, ze nechapu presne, co chces rict.

Zvedavec 4 · 10. 10. 2017 13:10

Jeste abych upresnil, co tim myslim.

Tedy to, ze celkovy vliv rychlosti pohybu prostorem musi byt spocitan pomoci $\Gamma ^{2}$ a ne jenom gamy samotne, ktera jenom vyjadruje jeho dva jakoby na sobe "nezavisle" efekty, tedy dilataci a kontrakci. Dilatace se spocita pomoci gamy a kontrakce se spocita pomoci stejne gamy a tedy konecny vysledek by mel byt docilen vynasobenim $\Gamma ^{2}$ .

Jako v tom priklade s podelnymi hodinami, vysledkem je $\Gamma ^{2}$ a abchom dostali jejich spravny cas, musime tu $\Gamma ^{2}$ vydelit gamou zpusobenou kontrakci. A tudiz dolet do vzdalenychh galaxii je umoznen tim, ze nejenom se cas cestovateli zkrati gamou, ale vzdalenost se taky zkrati gamou s celkovym ucinkem vzniklym gamou na druhou.

KennyMcCormick · 10. 10. 2017 16:12

↑ Zvedavec 4:

Ale neznamena todle, ze ty dva efekty, dilatace a kontrakce, pusobi oba soucasne

Ano.

tedy ze se nasobi

Ne. Oba efekty působí současně, ale nenásobí se. Počítá se to tak, jak napsal ↑ LukasM:.

Ze oboji ty hodiny, tedy pricny a podelny, musi ukazovat stejny cas je mi jasny. Ta $\Gamma$ , ktera vznika diky zkraceni podelnych hodin, a ktera ten jejich chod naopak zrychli s celkovym vysledkem, ze budou ukazovat stejne jako ty pricny, tedy celkove jenom $\Gamma$ -krat pomalejs nez hodiny v "nehybne soustave" na Zemi, a ktera ma vliv jenom na vysledny chod hodin, neni tedy zaroven dukazem, ze (...)

Není. Když napíšeš podrobněji, jak jsi k tomu došel, řekneme ti, kde máš chybu.

↑ Zvedavec 4:

Tohle je v prispevku "Einstein for Everyone" Johna D. Nortona, kde on tam udava takovy vysledek a prave si myslim, ze chce rict, ze vysledna $\Gamma$ se prave umocnuje. Jediny, co bych mohl, by bylo to sem okopirovat.

Nekopíruj to sem, ale dej odkaz, všechny kapitoly jsou tady: http://www.pitt.edu/~jdnorton/teaching/ … index.html

↑ Zvedavec 4:
Tohle už nedává smysl.

Zvedavec 4

↑ KennyMcCormick:

Kenny, diky za odpoved.

Tohle se zda byt spis filosoficky problem nez pouze matematicky a tak k tomu spis pristupuju. Snazim se STR vstrebat spis intuitivne i kdyz mnohdy az prilis jednoduche vzorce mne zatahnou i castecne do vypoctu.

Predpokladam totiz, a mozna spatne, ze kdyz, jako ty podelny hodiny, se neco zkrati "x" krat anebo se cas zpomali "x" krat a to v ramci uvah o STR, musi to byt automaticky vysledkem prepoctu gama.

Na pricnych hodinach se ten paprsek priblizi o 30 000km (tedy desetinu vteriny) k tomu druhemu zrcadlu kazdou vterinu odtikanou na hodinach na Zemi. To znamena, ze cas na nich tika 10x pomalejs nez na hodinach na Zemi.

Na podelnych hodinach se musi uvazovat s cestou tam a zpatky, protoze doba, za kterou je paprsek urazi neni stejna.

A proto se zda logicky, ze kdyz raketa leti 298 500km/s (presne 298 496.2311km/s ), kdy tedy gama=10 a hodiny jsou dlouhy 300 000km a c=300 000km/s, kdy tedy rozdil 300 000-298 500=1 500km (300 000-298 496.2311=1 503.768 869km) o kterych se paprsek priblizi druhemu zrcadlu kazdou vterinu ubehlou na hodinach na Zemi, potrva mu to 200 vterin(presnejc 199.498 743 6), nez k nemu doleti. Jelikoz aby doletel zpatky mu potrva pouhych 0.5 (0.498 743 71) vteriny (0.501 256 42), dva tiky tech podelnych hodin pak budou 200x pomalejsi nez dva tiky hodin na Zemi a skoro 200x pomalejsi nez jejich jeden tik (hodin na Zemi). Z toho se musi vzit prumer, tedy 200/2=100, presne jak to tam uvadi.

A tedy ty podelny hodiny se zdaji bezet 10x rychlejs nez ty pricny a 100x rychlejs nez ty na Zemi.

Ale protoze ani v STR (a ani mimo ni) neni pripustitelny aby hodiny umisteny v jedne rakete ukazovaly jiny cas, a to kvuli isotropii prostoru, jak tam vysvetluje, musi se rozdil mezi temihle vypocty nejak vysvetlit. A tudiz, zrejme Einstein sam, prisel s resenim, ze jak telesa v pohybu tak i prostor ktery preklenou se navic krati ve smeru jejich pohybu.

Proto jedinou moznou odpovedi se musi zdat, ze ten rozdil 10x mezi hodinami v rakete v nasem priklade znamena dalsi gamu, ktera je v tomhle priklade taky 10 a ktera se musi prisoudit prave tomu zkraceni prostoru po smeru letu. On to tak prece tvrdi, alespon tak tomu rozumim.

Tak si musim myslet, ze se ty dva vysledky, dilatace a kontrakce nasobi, tedy gama se umocni aby se dosahlo ccelkoveho efektu.

A to by tedy jasne ukazovalo, ze cesta k Andromede by trvala 40 let kosmonautovych pri pouhe game=224 pri rychlosti rychlosti "pouhych" 229 997 km/s a mionu by stacilo letet "pouhych" 297 880km/sec aby v pohode dorazil na zem namisto udanych 299 970.2425, protoze o zbytek nezbytneho efektu by se postaralo zkraceni trasy letu.

Takhle se taky bude zdat byt mnohem jednodussi doletet jednou az na konec vesmiru anebo ho dokonce i obletet behem zivot kosmonautu, o cem jsem se taky docet nekde, ale uz nevim kde, snad na wiki.

Kde je tedy chyba v tehle me uvaze?

Nemuzu tvrdit, ze to tak 100%-ne je, a proto ma puvodni otazka byla, jestlo to muze nekdo bud potvrdit anebo vyvratit?

Zvedavec 4 · 11. 10. 2017 21:28

Jo, ten odkaz. Je to prece presne tam s obrazkem tech hodin. Jak rikam, on tam netvrdi nic o game, to jen tak, a mozna mylne, predpokladam, ze tim mysli! Nechtel jsem Te splest.

Zvedavec 4 · 11. 10. 2017 22:09

Na podelnych hodinach se musi uvazovat s cestou tam a zpatky, dva tiky hodin tech podelnych pak budou 200x pomalejsi nez jeden tik hodin na Zemi. Z toho se musi vzit prumer, tedy 200/2=100, presne jak to tam uvadi.

A tedy ty podelny hodiny se zdaji bezet 10x rychlejs nez ty pricny a bezi 100x rychlejs nez ty na Zemi.

Jeste se to musi upresnit: "....dva tiky hodin tech podelnych pak budou 200x pomalejsi nez dva tiky hodin na Zemi a skoro 200x pomalejsi nez jeden tik hodin na Zemi...."

LukasM · 12. 10. 2017 11:02 — Editoval LukasM (12. 10. 2017 11:02)

Zvedavec 4 napsal(a):
Tohle se zda byt spis filosoficky problem nez pouze matematicky a tak k tomu spis pristupuju. Snazim se STR vstrebat spis intuitivne i kdyz mnohdy az prilis jednoduche vzorce mne zatahnou i castecne do vypoctu.

To bude možná ta chyba. Tohle intuitivní není, a málokdo to tak může pochopit.

Zvedavec 4 napsal(a):
Predpokladam totiz, a mozna spatne, ze kdyz, jako ty podelny hodiny, se neco zkrati "x" krat anebo se cas zpomali "x" krat a to v ramci uvah o STR, musi to byt automaticky vysledkem prepoctu gama.

No, on koeficient gama je právě tak definovaný. V Lorentzových transformacích se objevuje podivná odmocnina ve jmenovateli, která se značí symbolem gama.

Zvedavec 4 napsal(a):
Na pricnych hodinach se ten paprsek priblizi o 30 000km (tedy desetinu vteriny) k tomu druhemu zrcadlu kazdou vterinu odtikanou na hodinach na Zemi. To znamena, ze cas na nich tika 10x pomalejs nez na hodinach na Zemi.

Desetina sekundy to je při pohledu z lodi. Čas na nich je pomalejší při pohledu ze Země.

Zvedavec 4 napsal(a):
Na podelnych hodinach se musi uvazovat s cestou tam a zpatky, protoze doba, za kterou je paprsek urazi neni stejna.

Při pohledu ze Země.

Zvedavec 4 napsal(a):
...(dlouhý odstavec)...
A tedy ty podelny hodiny se zdaji bezet 10x rychlejs nez ty pricny a 100x rychlejs nez ty na Zemi.

Podélné hodiny běží 10x POMALEJI než příčné, a to z pohledu pozorovatele na Zemi. Příčné běží 100x POMALEJI než ty na Zemi při pohledu pozorovatele na Zemi. Tak by to alespoň bylo, kdyby neexistovala kontrakci délek (a je to ve sporu s principem relativity). To podivné průměrování bych vypustil, tady to nevadí, ale budí to dojem, že při pohledu ze Země trvá světlu cesta od jednoho zrcadla je druhému 100s, což není pravda (jak jsi sám spočítal). Odraz od předního zrcadla při pohledu ze Země nenastane v polovině času cesty tam a zpět, zatímco při pohledu z lodi ano. Je lepší jako jeden tik hodin uvažovat cestu tam a zpět, a porovnávat soumístné události.

Zvedavec 4 napsal(a):
Ale protoze ani v STR (a ani mimo ni) neni pripustitelny aby hodiny umisteny v jedne rakete ukazovaly jiny cas, a to kvuli isotropii prostoru, jak tam vysvetluje, musi se rozdil mezi temihle vypocty nejak vysvetlit. A tudiz, zrejme Einstein sam, prisel s resenim, ze jak telesa v pohybu tak i prostor ktery preklenou se navic krati ve smeru jejich pohybu.

Ano, to je jeden ze způsobů jak kontrakci délek zavést, tedy na základě principu relativity. Jiný způsob (a velmi silný) spočívá v tom, že když se bude čas a délka transformovat podle STR (Lorentzovou transformací), budou Maxwelllovy rovnice invariantní, a tedy v souladu s principem relativity.

Zvedavec 4 napsal(a):
Proto jedinou moznou odpovedi se musi zdat, ze ten rozdil 10x mezi hodinami v rakete v nasem priklade znamena dalsi gamu, ktera je v tomhle priklade taky 10 a ktera se musi prisoudit prave tomu zkraceni prostoru po smeru letu.

To není žádná "další" gama. Prostě se řekne, že podélné vzdálenosti se zkracují ve stejném poměru, o kolik pomaleji plyne čas. Tj. gama-krát.

Zvedavec 4 napsal(a):
Tak si musim myslet, ze se ty dva vysledky, dilatace a kontrakce nasobi, tedy gama se umocni aby se dosahlo ccelkoveho efektu.

Ale jakého celkového efektu? Co chceš spočítat? Při pohledu zvenku se prostě vzdálenosti zkrátí faktorem gama a časový odstup soumístných událostí se prodlouží faktorem gama (obojí oproti klidové soustavě). Co se přitom vynásobí nebo zkrátí záleží na tom, co s těmi veličinami děláš. Pokud se díváš na podélné světelné hodiny ze soustavy Země, zkrátíš vzdálenost gama krát. Světlo je pořád světlo (ve všech soustavách), takže mu to neublíží.

Zvedavec 4 napsal(a):
... a mionu by stacilo letet "pouhych" 297 880km/sec aby v pohode dorazil na zem namisto udanych 299 970.2425, protoze o zbytek nezbytneho efektu by se postaralo zkraceni trasy letu.

Nesmysl. Rozlišuj v jaké soustavě pracuješ.

Pokud toto bude číst KennyMcCormick nebo někdo podobně znalý, prosím raději o kontrolu a případné doplnění. Jakkoli si myslím, že tomu rozumím, chybu jsem udělat mohl a něco říct nepřesně také.

Zvedavec 4 · 12. 10. 2017 21:19

LukasM napsal(a):
Zvedavec 4 napsal(a):
Proto jedinou moznou odpovedi se musi zdat, ze ten rozdil 10x mezi hodinami v rakete v nasem priklade znamena dalsi gamu, ktera je v tomhle priklade taky 10 a ktera se musi prisoudit prave tomu zkraceni prostoru po smeru letu.
To není žádná "další" gama. Prostě se řekne, že podélné vzdálenosti se zkracují ve stejném poměru, o kolik pomaleji plyne čas. Tj. gama-krát.

Zvedavec 4 napsal(a):
Tak si musim myslet, ze se ty dva vysledky, dilatace a kontrakce nasobi, tedy gama se umocni aby se dosahlo ccelkoveho efektu.
Ale jakého celkového efektu? Co chceš spočítat? Při pohledu zvenku se prostě vzdálenosti zkrátí faktorem gama a časový odstup soumístných událostí se prodlouží faktorem gama (obojí oproti klidové soustavě). Co se přitom vynásobí nebo zkrátí záleží na tom, co s těmi veličinami děláš. Pokud se díváš na podélné světelné hodiny ze soustavy Země, zkrátíš vzdálenost gama krát. Světlo je pořád světlo (ve všech soustavách), takže mu to neublíží.

Beru to tak, ze protoze 100 nasobne zpomaleni vuci casu na Zemi podelnych hodin jako i jejich 10-ti nasobne zpomaleni vuci hodinam pricnym je matematicky spocitano, tedy skutecnost, ktera jenom dava podnet k otazce, cim to muze byt zpusobeno a k predpokladu, ze se tedy krati vzdalenosti po smeru letu, nemuze se rict, ze neexistuje.

Memu chapani tedy, protoze tam ta umocnena gama je spocitana, a jeji cast je jenom prevedena na vysvetleni jineho ukazu, ma otazka znela, jestli dilatace a kontrakce spolu vynasobene jsou soucasti gamy anebo se v celkovem efektu musi jejich vliv teprv umocnit.

Z prikladu s mionem je asi jasne, ze ten celkovy efekt uz je zapocitany v zakladni game, tedy gama je vlastne 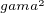$_{gama^{2}}$ .

V priklade s podelnyma hodinama se to zda naopak, protoze gama, co ma byt 100, se rozdeli na dve casti, tedy 10x10=100. Protoze ta kontrakce rusi cast casoveho efektu, mela by se projevovat misto nej aby se vysledek, ktery se spocital coby 100x, zachoval.

Vysvetleni, ze protoze se zrcadla 10x sobe priblizi a tudiz vzdalenost, kterou paprsek musi urazit, se 10x zkrati a tudiz vysledna vysledna gama je pouze 10, ale neodpovida vypoctu, ze vysledny efekt je vlastne 100nasobny.

V priklade s Andromedou, se tedy vzdalenost kosmonautovi v rakete jenom jevi, ze se krati. Jelikoz nema zadny zpusob jak si porovnat rychlost plynuti jeho casu s jinou soustavou, musi si nejak vysvetlit, proc se k ni priblizuje rychlejs nez by mel.

Moc se mi to nezda, protoze se tim uplne zanedbava, co se spocitalo. Protoze, kdyz vypocet rika, ze se tam neco deje 100x, ale prepocet se pak bere jenom 10x a zbytek se odmitne. Protoze, kdyz se tech 10x prisuzuje jinemu ukazu, tedy kraceni, mely by se ty dva efekty nasobit, bych si myslel.

Cili, aby Andromedu dosahnul za 40 let sveho zivota bude muset kosmonaut letet rychlosti odpovidajici game rovne 50 000. To snad nebude technicky nikdy mozne. Ale musim tomu verit.

KennyMcCormick · 12. 10. 2017 22:22

↑ Zvedavec 4:

Jo, ten odkaz. Je to prece presne tam s obrazkem tech hodin.

Tam není žádný obrázek hodin. :) Napiš název kapitoly.

↑ Zvedavec 4:

A proto se zda logicky, ze kdyz raketa leti 298 500km/s (presne 298 496.2311km/s ), kdy tedy gama=10 a hodiny jsou dlouhy 300 000km a c=300 000km/s, kdy tedy rozdil 300 000-298 500=1 500km (300 000-298 496.2311=1 503.768 869km) o kterych se paprsek priblizi druhemu zrcadlu kazdou vterinu ubehlou na hodinach na Zemi, potrva mu to 200 vterin(presnejc 199.498 743 6), nez k nemu doleti. Jelikoz aby doletel zpatky mu potrva pouhych 0.5 (0.498 743 71) vteriny (0.501 256 42), dva tiky tech podelnych hodin pak budou 200x pomalejsi nez dva tiky hodin na Zemi a skoro 200x pomalejsi nez jejich jeden tik (hodin na Zemi).

Zapomněl jsi, že podélné hodiny budou relativisticky zkrácené ve směru pohybu na 1/10 původní délky, takže doba tiku vyjde 10krát kratší (20 s, ne 200 s). Doba tiku hodin na Zemi je 2 s. Podélné hodiny jdou 10krát pomaleji než hodiny na Zemi a stejně rychle jako hodiny příčné.

↑ Zvedavec 4:

Beru to tak, ze protoze 100 nasobne zpomaleni vuci casu na Zemi podelnych hodin jako i jejich 10-ti nasobne zpomaleni vuci hodinam pricnym je matematicky spocitano, tedy skutecnost, ktera jenom dava podnet k otazce, cim to muze byt zpusobeno a k predpokladu, ze se tedy krati vzdalenosti po smeru letu, nemuze se rict, ze neexistuje.

Příčné i podélné hodiny jdou stejně rychle.

Zvedavec 4 · 12. 10. 2017 23:44

Kenny, muj dotaz o dilataci vs. kontrakci se toci jenom kolem toho, tedy co udava ten John Norton v kapitole "Clocks and Rods", kde vysvetluje snad to nejelementarnejsi pojeti principu STR.

LukasM · 13. 10. 2017 16:38 — Editoval LukasM (13. 10. 2017 16:39)

↑ Zvedavec 4:
Ja mam pocit, ze jsme se nejak zacyklili. Jak ja, tak KennyMcCormick jsme k tomu napsali rekl bych dost. Dokazes rict, s cim mas jeste problem? Idealne bez tapetovacich prispevku, treba maximalne peti vetami? Proste pri pozorovani pohybujicich se hodin je uvidim zkracene a zpomalene. A jak je na te strance vysvetleno, plati to pro hodiny libovolne konstrukce a plyne to ze stalosti rychlosti svetla a principu relativity. Kde je problem?

KennyMcCormick · 13. 10. 2017 19:45

↑ Zvedavec 4:

Kenny, muj dotaz o dilataci vs. kontrakci se toci jenom kolem toho, tedy co udava ten John Norton v kapitole "Clocks and Rods", kde vysvetluje snad to nejelementarnejsi pojeti principu STR.

I tam píše, že příčné i podélné hodiny jdou stejně rychle. :)

Jestli je v té kapitole něco, o čem se ti zdá, že to protiřečí něčemu, co píšeme, zkopíruj sem konkrétní větu z jeho stránek a můžeme ti to vysvětlit na té konkrétní větě.

Zvedavec 4 · 14. 10. 2017 15:43

Mym problemem nejsou zakladni pojeti STR jako dilatace a kontrakce. Alespon ne jejich zakladni pochopeni. Ani jsem neodmital logickou skutecnost, ze oboje ty hodiny musi bezet stejne rychle. Ale vzdycky mne lamalo hlavou, jestli tyhle dva konkretni efekty pusobi nezavisle, tedy se pri konecne uvaze musi vzajemne vynasobit anebo jestli uz jsou oba zahrnuty v prepoctu gama.

Muzu rict, ze po hlubsi rozvaze na popud vasich "neustupnych" postoju k veci musim prijmout to, ze uz jsou oba ty efekty v ty game zahrnuty. Protoze, jak Lukas zduraznil, jak se podelne hodiny zkracuji potrva paprsku kratsi dobu dosahnout toho druheho zrcadla a tim se, jenom tedy zdanlive a dodatecne zpomaleni jejich chodu z pohledu pozorovatele v "nehybne" soustave na Zemi, automticky vyrusi.

Bohuzel se tim moznost docileni vzdalenych galaxii lidstu podstatne ztezuje, a to primo nadruhou.

Zvedavec 4 · 14. 10. 2017 15:58

Jsem rad, ze jsem si byl diky tomu schopen vyjasnit tenhle zdanlivy rozpor v STR.

KennyMcCormick · 14. 10. 2017 18:13

Jestli je už jasné, jak a proč se to všechno počítá, je to skvělé.

Hodně štěstí s dalším zájmem o fyziku. :)

Matematické Fórum

#1 09. 10. 2017 16:01

Dilatace casu vs. Kontrakce delek

#2 09. 10. 2017 16:41

Re: Dilatace casu vs. Kontrakce delek

#3 09. 10. 2017 17:22

Re: Dilatace casu vs. Kontrakce delek

#4 09. 10. 2017 18:26 — Editoval LukasM (09. 10. 2017 18:29)

Re: Dilatace casu vs. Kontrakce delek

#5 10. 10. 2017 02:34

Re: Dilatace casu vs. Kontrakce delek

#6 10. 10. 2017 02:40

Re: Dilatace casu vs. Kontrakce delek

#7 10. 10. 2017 12:21

Re: Dilatace casu vs. Kontrakce delek

#8 10. 10. 2017 13:10

Re: Dilatace casu vs. Kontrakce delek

#9 10. 10. 2017 16:12

Re: Dilatace casu vs. Kontrakce delek

#10 11. 10. 2017 21:21 — Editoval Zvedavec 4 (12. 10. 2017 02:03)

Re: Dilatace casu vs. Kontrakce delek

#11 11. 10. 2017 21:26 Příspěvek uživatele Zvedavec 4 byl skryt uživatelem Zvedavec 4. Důvod: Editoval jsem ten original

#12 11. 10. 2017 21:28

Re: Dilatace casu vs. Kontrakce delek

#13 11. 10. 2017 22:09

Re: Dilatace casu vs. Kontrakce delek

#14 12. 10. 2017 11:02 — Editoval LukasM (12. 10. 2017 11:02)

Re: Dilatace casu vs. Kontrakce delek

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

#15 12. 10. 2017 21:19

Re: Dilatace casu vs. Kontrakce delek

LukasM napsal(a):

Zvedavec 4 napsal(a):

Zvedavec 4 napsal(a):

#16 12. 10. 2017 22:22

Re: Dilatace casu vs. Kontrakce delek

#17 12. 10. 2017 23:44

Re: Dilatace casu vs. Kontrakce delek

#18 13. 10. 2017 16:38 — Editoval LukasM (13. 10. 2017 16:39)

Re: Dilatace casu vs. Kontrakce delek

#19 13. 10. 2017 19:45

Re: Dilatace casu vs. Kontrakce delek

#20 14. 10. 2017 15:43

Re: Dilatace casu vs. Kontrakce delek

#21 14. 10. 2017 15:58

Re: Dilatace casu vs. Kontrakce delek

#22 14. 10. 2017 18:13

Re: Dilatace casu vs. Kontrakce delek

Zápatí