Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Poměry obsahů trojúhelníků v lichoběžníku (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 10. 2017 18:41
Poměry obsahů trojúhelníků v lichoběžníku
Ahoj,
Mám takový menší problém s výpočtem obsahů trojúhelníků uvnitř lichoběžníku, které musím následně porovnat.
Zadání příkladu zní asi takto: lichoběžník ABCD, znám délku strany AB=25cm, pak délku úhlopříčky AC=12cm, také vím kolik měří část této úhlopříčky předtím, než protne úhlopříčku BD (tento bode se jmenuje O), u které zase znám jen její část po protnutí, tj. blíže k bodu D a je to 3cm. Mám vypočítat kolik je zbytek úhlopříčky BD a také, kolik je délka úsečky CD.. Následně mám porovnat obsah trojúhelníku ABO s trojúhelníkem obsahem CDO. Poté porovnat obsah ABO s obsahem BCO, pak porovnat obsah ABO s obsahem ADO a nakonec porovnat obsah BCO s obsahem ADO. U všecho mám udělat poměr.
Problém je v tom, že se mi sice povedlo získat délky úseček CD a BO, ale tím jsem skončil. Nedokážu vypočítat obsah jediného trojúhelníku. Vychází mi výška nula.
Jsem v koncích. Můžete mi prosím někdo pomoci?
PS: přikládám nákres: https://ibb.co/h0WMbG
Offline
- (téma jako vyřešené označil(a) bemtom)
#8 10. 10. 2017 20:32 — Editoval misaH (10. 10. 2017 20:37)
- misaH
- Příspěvky: 13459
Re: Poměry obsahů trojúhelníků v lichoběžníku
↑ bemtom:
No - stačí vedieť, že keď koeficient podobnosti je  , tak zmena obsahu je
, tak zmena obsahu je  .
.
Trikrát väčší trojuholník stranami znamená deväťkrát väčší trojuholník obsahom.
A nielen u trojuholníka.
Všetky úsečky sú väčšie k-krát, teda aj výška, to je tá príčina. Dá sa to aj pekne nakresliť.
Offline
#10 11. 10. 2017 08:33
Re: Poměry obsahů trojúhelníků v lichoběžníku
Nejsem si jisty, jestli rozumim zadani. Zkus treba priste zvyraznit cervenou pastelkou, co znas ze zadani. Zbytek je jasne, ze jsi nejak vypocital.
troj CDO je podobny ABO, protoze se zrcadli pres O se zvetsovanim. Vmi, neni to moc matematicky receno. Pak plati, ze nasobek stran je stejny, treba k.
a = k * c
u1_1 = k* u1_2
u2_1 = k* u2_2
v1 = k * v2
S1 = a * v1 = k * c * k * v2
S2 = c * v2 = c * v2
S1 / S2 = k * k * 1
Kdybych tohle vsechno nevedel a vychazel jen z obrazku.
uhel ODC (uhel1) je stejny jako OBA (uhel1). Totez dalsi uhel.
sin(uhel1) = v2 / u2_2
sin(uhel1) = v1 / u2_1
v2 / u2_2 = v1 / u2_1
v1 = u2_1/u2_2 * v2
sin(uhel2) = v2 / u1_2
sin(uhel2) = v1 / u1_1
v2 / u1_2 = v1 / u1_1
v1 = u1_1/u1_2 * v2
Kdyz to das oba vysledky do rovnice dostanes, ze pomery uhlopricek jsou stejne
u2_1/u2_2 = u1_1/u1_2
Takze uz znas pomer uhlopricek, z toho snadno ziskas u2_2 (x). Pak v1 (va). v2.
Z v2 c uz nejak vypocitas, ne?
Offline
#13 11. 10. 2017 16:50
Re: Poměry obsahů trojúhelníků v lichoběžníku
↑ misaH:
Nula mi vychází, když použiju rovnost výšky trojuhelniku ABO. Asi takto, vzdálenost protnutí výškou Vo strany AB je x od bodu A, takže vzdálenost od bodu B je 25 (délka celé strany AB) - x. Takže když provedu rovnost ->
10^2 - x^2 = 15^2 - (25-x)
Výjde, že x = 10, jenže, když dosadím za x, tak vznikne: 10^2 - 10^2 = Vo —> tzn. 0
Offline
#14 11. 10. 2017 16:57
Re: Poměry obsahů trojúhelníků v lichoběžníku
Vzhledem k tomu, že 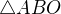 a
a 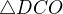 jsou si tedy podobné a je to poměr 5:1, tak obsahy S1 a S2 jsou 25:1, protože jak už zmínil misaH, že obsah je k^2.
jsou si tedy podobné a je to poměr 5:1, tak obsahy S1 a S2 jsou 25:1, protože jak už zmínil misaH, že obsah je k^2.
Myslím si, že pointa toho všeho je, že tyto dva jsou si podobné a tato úvaha jde použít, ale druhé dva trojúhleníky, které v lichoběžníku jsou, konkrétně 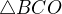 a
a 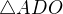 si nejsou podobné spolu a ani s ostatními. To tedy musí znamenat, že žádný poměr udělat nemohu? Je to tak?
si nejsou podobné spolu a ani s ostatními. To tedy musí znamenat, že žádný poměr udělat nemohu? Je to tak?
Offline
#15 11. 10. 2017 17:26
Re: Poměry obsahů trojúhelníků v lichoběžníku
↑ bemtom:
pokud troj. nejsou podobné, neexistuje poměr podobnosti. Ale poměr obsahů dvou rovinných útvarů můžeš vypočítat vždy. Můžeš se třeba ptát, kolik procent obsahu čtverce zaujímá jemu vepsaný kruh. A v tom případě pracuješ s podílem, t.j. poměrem obsahů. Takže se snaž dál.
Offline
#20 11. 10. 2017 21:19 — Editoval misaH (11. 10. 2017 21:21) Příspěvek uživatele misaH byl skryt uživatelem misaH.
#22 12. 10. 2017 07:31
Re: Poměry obsahů trojúhelníků v lichoběžníku
↑ Al1:
Dobře to by dávalo smysl, nenapadlo mě na to ani pomyslet.
Ale musí to tedy být tak, že poměr stran trojuhelnika ABO s trojuhelnikem CDO je 5:1, můžete někdo prosím potvrdit, že je tento závěr správný? Došel jsem k němu tak, že jsem úhlopříčku, u které znám celou její délku což je 12cm a znám i její část před O a za O což je 10 a 2, dělil jsem 10:2 a mám poměr 5:1, poté jsem dopočítal zbytek. Je to správně?
Offline
#24 12. 10. 2017 08:33
Re: Poměry obsahů trojúhelníků v lichoběžníku
↑ Al1:
Takže je tedy definitivem, že trojúhelníky nemohou existovat, protože součet dvou stran je menší, respektive je roven straně třetí, konkrétně je to 10+15=25 a základna (třetí strana) je 25.
Takže proto výška vychází 0 a celý příklad nemá řešení.
Je to správný závěr?
Offline
#25 12. 10. 2017 09:11 — Editoval Al1 (12. 10. 2017 09:22)
Re: Poměry obsahů trojúhelníků v lichoběžníku
↑ bemtom:
ano, po výpočtu rozměrů troj ABO a CDO na základě poměru podobnosti jsi zjistil, že dané trojúhelníky neexistují, protože neplatí trojúhelníková nerovnost: součet délek dvou stran není větší než délka třetí strany. Takto zadaná úloha není dále v otázkách porovnání obsahů trojúhelníků řešitelná.
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Poměry obsahů trojúhelníků v lichoběžníku (TOTO TÉMA JE VYŘEŠENÉ)

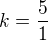 (poměr
(poměr 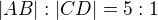 )
)