Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 10. 2017 17:20
Slovní úloha prosím o pomoc
Dobrý den všem.Dostala jsem zadání: mám válec s V=1l, mám vypočítat povrch tak, aby byl minimální. Dostali jsme i obrázek výpočtu učitele, kde ale V je taky neznámá. Vůbec tam nechápu ani úpravení toho výrazu. Vím teoreticky jak na to, ale vůbec mi to nevychází. Děkuju všem
Offline
#2 24. 10. 2017 17:58
Re: Slovní úloha prosím o pomoc
↑ Regina:
Dobrý den,
použijte základní vzorce pro válec: 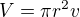 a
a 
Ze vzorce pro objem si vyjádřete  a dosaďte do vzorce pro povrch.
a dosaďte do vzorce pro povrch.
Potom vzorec pro povrch derivujte podle  a tuto derivaci položte rovnu 0.
a tuto derivaci položte rovnu 0.
Takto zjistíte optimální poloměr  a dopočtěte
a dopočtěte  .
.
Je třeba si ale ověřit, zda se jedná o lokální minimum. Nejlépe druhou derivací funkce pro povrch a dosazením vypočteného  .
.
Offline
#3 25. 10. 2017 12:31
Re: Slovní úloha prosím o pomoc
↑ Regina:
já tady jen doplním kolegyni a rozepíšu, co tím vším myslela, protože jsi problém neoznačila za vyřešen, čiže možná ještě stále tápeš.
je zadán tedy válec o objemu jednoho litru a tvým úkolem ze zadání bylo určit jeho rozměry (poloměr a výšku) tak, aby jeho povrch byl minimální, předpokládám. Dotaz nedával úplně smyslu. Povrch spočítat lze, ale ne tak, aby byl minimální, k tomu nám pomůže vhodná volba rozměrů.
Minimum pro:
(*) S = 2*pi*r^2 + 2*pi*r*v
tady víš, že:
(**) 1 = pi*r^2*v
r je pak poloměr a v výška válce.
Tady si vytáhneme výšku válce v závislosti na poloměru (**) vzorcem:
v = 1/(pi*r^2)
a dosadíme do vzroce pro povrch (*) :
(***) S = 2*pi*r^2 + 2*pi*r*(1/(pi*r^2)) = 2*pi*r^2 + 2/r
Tady je třeba povrch S minimalizovat a upravený vzorec pro jeho výpočet (***) je vlastně reálná funkce jedné proměnné (r). Musíme tedy zjistit, kde má minimum. To je místo, kde má nulovou první derivaci a kladnou druhou derivaci.
čiže první derivace:
S' = 4*pi*r - 2 / r^2
je nulová pro r rovno
4*pi*r - 2/r^2 = 0
4*pi*r^3 = 2
r = odm3(1/(2*pi)) = 1/odm3(2*pi)
Druhá derivace je vždy kladná (pro kladný poloměr), a tak ji nemusíme vlatně ani konkrétně hledat.
Z () dopočítáme i výšku **v
v = 1/(pi*r^2) = odm3(2*pi)^2 * / pi = odm3(4) / odm3(pi) = odm3(4/pi)
A matematika je věda, kde si můžeme vše zpětně ověřit, proto pro kontrolu spočítáme objem s našimi hodnotami:
V = pi*r^2*v = pi*odm3(4/pi) / odm3(2*pi)^2 = pi*odm3(4/(4*pi^3)) = pi / pi = 1
Kontrola proběhla, jak vidíš, v pořádku, proto můžeme udat výsledky:
r = odm3(1/(2*pi)) dm
v = odm3(4/pi) dm
v decimetrech, protože jsme v nich udávali i objem - litr je pak dm3, jak jistě víš.
výpočet druhé derivace ještě:
S'' = (4*pi*r - 2/r^2)' = 4*pi + 4*r / r^4 = 4*pi + 4/r^3
první sčítanec je konstanty (kladná) a druhý je pro poloměr větší než nula, je vždy kladný, takže výsledek musí být kladné číslo. Znamená to, že funkce počítající povrch v závislosti na poloměru je všude konvexní. V tomhle případě se jedná o parabolu tedy.
Stejný postup by šlo spočítat i v případě, že objem válce neznáš. Dostali bychom pak informaci, v jakém poměru nastavit jeho poloměr a výšku tak, aby byl jeho povrch (při zachování objemu) co nejmenší. O což se možná snažila tvá kantorka, proto Vám zadal neznámou V ještě navíc.
Kolega, kolegyně Takjo mě může doplnit či překontrolovat. Jinak jsem s pozdravem :) Je fajn, že tohle forum pro studenty existuje.
Offline


![kopírovat do textarea $d=v=\sqrt[3]{\frac{4V}{\pi }}$](/mathtex/a7/a79d6d5e286fddd3fbad0a6239386e8c.gif)
 zkuste LaTeXový editor.
zkuste LaTeXový editor. Omlouvám se nejsem na matiku dobrá
Omlouvám se nejsem na matiku dobrá