Matematické Fórum

berpauli · 13. 05. 2009 21:51

proč ten priklad se nezobrazi tak jak ma..

Alivendes · 13. 05. 2009 21:51

a to druhé stejně tak...pokud neznáš argument x u xlog a tk stím nic dělat nejde...

svatý halogan · 13. 05. 2009 21:51

↑↑ Alivendes:

Tím se akorát dostaneš zpět k zadání.

berpauli · 13. 05. 2009 21:52

↑↑ svatý halogan:
tady jsem se prave zasekla..sem tomu rozumim ..ale dal newim

svatý halogan · 13. 05. 2009 21:53

↑ berpauli:

Použij nabízenou substituci.

O.o · 13. 05. 2009 21:55 — Editoval O.o (13. 05. 2009 21:55)

↑ berpauli:

Jestli tím zobrazením myslíš $\text{toto, tak si zobraz tento prispevek jako citaci a uvidis, ze ti chybi kolem tveho vyrazu hranate zavorky s tagy tex a /tex.}$ Pokud jde ovšem o něco jiného, tka se omlouvám a příspěvek nakonec nějak smažu..

berpauli · 13. 05. 2009 21:57

$To je ono..:D..dekuji$

O.o · 13. 05. 2009 21:58

↑ berpauli:

Když píšeš text a ne matematický zápis příkladu, tak celý text uzavři do \text{Sem piš text}, tím se ti nebdue zobrazovat italicem a budou se ti dělat mezery, podle mezerníku (space), oki?

berpauli · 13. 05. 2009 22:07

↑ O.o:
ok

berpauli · 13. 05. 2009 22:12

↑ svatý halogan:

a kdy to vlastne muzu zlogaritmovat?

O.o · 13. 05. 2009 22:14

↑ berpauli:

Což o to, zlogaritmovat to vlastně můžeš kdy chceš, jen musíš postupovat obezřetně ;-).

mák · 14. 05. 2009 02:49 — Editoval mák (14. 05. 2009 02:54)

Toto téma je opravdu zajímavé. Já to tam neviděl. Tedy myslím tento trik:
$3+\sqrt{8}=(3+\sqrt{8}) \cdot 1 = (3+\sqrt{8}) \cdot \frac{3-\sqrt{8}}{3-\sqrt{8}}=\frac{1}{3-\sqrt{8}}$

Zkoušel jsem za jakých podmínek jej lze použít a zjistil jsem, že čísla musí splňovat určité přesné požadavky.
Takže tento příklad je záměrně takto napsaný a kdo jej nezná, ten asi těžko pochodí.
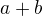Pokud si číslo $3+\sqrt{8}$ rozdělím na dvě části $a+b$ pak musí platit $a^2-b^2=1$ , jinak to nefunguje.

Takže v původní rovnici:
$(3-\sqrt{8})^x + (3+\sqrt{8})^x = 34$
Využijeme výše uvedeného triku a rozdílný základ nahradíme za stejný:
$(3-\sqrt{8})^x + (3-\sqrt{8})^{-x} = 34$
$(3-\sqrt{8})^x + \frac{1}{(3-\sqrt{8})^x} = 34$
Provedeme substituci:
$(3-\sqrt{8})^x=t$
$t + \frac{1}{t} = 34$
Odstraníme zlomek:
$t^2 + 1 = 34t$
A řešíme kvadratickou rovnici:
$t^2 - 34t + 1 = 0$
Máme dva kořeny:
$t_1=17-12\,\sqrt{2}\nlt_2=17+12\,\sqrt{2}$

Je jedno, který použijeme a dosadíme místo "t" původní výraz:
$(3-\sqrt{8})^x=17+12\,\sqrt{2}$
(S druhým nám vyjde to samé, ale s obrácenými znaménky).

Tady použijeme oblíbené logaritmování:
$x_1=\frac{\log$17-12\,\sqrt{2}$}{\log$3-\sqrt{8}$}\nlx_2=\frac{\log$17+12\,\sqrt{2}$}{\log$3-\sqrt{8}$}$
A výsledek dává docela hezké číslo:
$x_1=2\nlx_2=-2$