Matematické Fórum

Janisek · 27. 10. 2017 22:20

Ahoj,
mám spočítat objem tělesa, které je ohraničeno plochami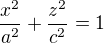
$\frac{x^{2}}{a^{2}}+\frac{z^{2}}{c^{2}}=1$
$y=\frac{b}{a}x$
$y=0$
$z\ge 0$
$x\ge 0$
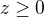
Použiju k tomu dvojný integrál a transformaci na polární souřadnice. Jelikož to těleso je ohraničené eliptickou válcovou plochou a rovinou, použiju zobecněné polární souřadnice.
Tedy: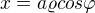
$x=a\varrho cos\varphi$
$y=b\varrho sin\varphi$
$|J|=ab\varrho$
Teď bych měl určit meze pro $\varphi$ a $\varrho$
Budou takto?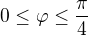
$0\le \varphi \le \frac{\pi }{4}$
$a\le \varrho \le \sqrt{a^{2}+b^{2}}$
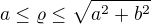
Díky moc..

Janisek · 28. 10. 2017 19:50

..prosím..

Jj · 28. 10. 2017 21:04

↑ Janisek: T5

Dobrý den.

Pro mě je to poněkud zamotané. Ještě předpokládám, že a, b, c > 0. Pak bych řekl, že:

$dV = y\,z\, dx$

$V = \int_0^a yz\,dx=\cdots =\frac{bc}{a^2} \int_0^a x\sqrt{a^2-x^2}\, dx = \cdots$

Matematické Fórum

#1 27. 10. 2017 22:20

Objem tělesa - dvojný integrál

#2 28. 10. 2017 19:07 Příspěvek uživatele Janisek byl skryt uživatelem Janisek.

#3 28. 10. 2017 19:50

Re: Objem tělesa - dvojný integrál

#4 28. 10. 2017 21:04

Re: Objem tělesa - dvojný integrál

Zápatí