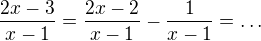Matematické Fórum

dawson · 02. 11. 2017 14:29 — Editoval dawson (02. 11. 2017 14:30)

Zdravím,
potřebuji poradit jak početně(bez grafu) určit obor hodnot např. u tohodle příkladu: $y= \frac{2x-3}{x-1}$

Děkuji za pomoc.

Ferdish

Je možné ten predpis upraviť tak, aby si z čitateľa odstránil premennú x a ostalo ti tam len číslo (konštanta)?

Potom už len pouvažuj nad tým, aký je obor hodnôt lineárne lomenej funkcie s konštantou v čitateli, a čo ti s ním urobí ten zvyšok, ktorý vznikol tou úpravou.

dawson · 02. 11. 2017 14:55

↑ Ferdish:
Omlouvám se, ale nechápu to.. :/ :)
Upravit to mám takhle? $y=\frac{2-3}{x-1}$
a dál? :)

Ferdish

↑ dawson:
Nemôžeš predsa z predpisu len tak škrtnúť premennú, kedy sa ti zachce - všetko má svoje pravidlá! Tak teda inak:

$\frac{2x-3}{x-1}=\frac{2x-2}{x-1}-\frac{1}{x-1}=\ldots$

dawson · 02. 11. 2017 15:20

↑ Ferdish:
takže, pokračoval jsem takto: 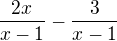$\frac{2x}{x-1}-\frac{3}{x-1}$ , z čehož jsem usoudil, že obor hodnot je R kromě -1.
Je to správně?

LukasM · 02. 11. 2017 15:35

↑ dawson:
Taková úprava je sice platná, ale spíš než k výsledku tě posouvá zpátky k zadání. ↑ Ferdish: tu svou úpravu dělal za nějakým účelem.... Zkus třeba z prvního zlomku vytknout dvojku.

A z toho tvého tvaru určitě neplyne, že obor hodnot je to, co píšeš. Ujasni si, jestli si nepleteš definiční obor a obor hodnot. Definiční obor jde určit přímo ze zadání, tam není třeba nic upravovat.

dawson · 02. 11. 2017 15:47

↑ LukasM:
Mám to, vytknul jsem dvojku a zkrátil závorky, poté mi hned došlo, že obor hodnot jsou reálná čísla kromě dvojky, a to jsem du téměř jistý :) Je to správně? .. a mimochodem Definiční obor jsou reálná čísla kromě jedničky. To jsem věděl. :) jinak Děkuji moc za pomoc :)

Ferdish · 02. 11. 2017 16:44

↑ dawson:
Niet za čo. Ale nebol som ďaleko od presvedčenia, že si iba troll :D

dawson · 02. 11. 2017 16:52

↑ Ferdish:

Jako, že jsem uplnej deb*l? :D to jsi mě potěšil.. jinak ještě jednou díky. :)

Ferdish · 02. 11. 2017 17:06

↑ dawson:
Zle si ma pochopil, nemal som v úmysle urážať tvoj intelekt. Čo sa týka adeptov na tebou spomenutý stupeň duševnej zaostalosti - na to sú tu iní.

Ale už sme úplne OT, takže by som to nechal tak. Tak či tak, tvoj matematický problém je vyriešený - obráťme list ;)

Matematické Fórum

#1 02. 11. 2017 14:29 — Editoval dawson (02. 11. 2017 14:30)

Obor Hodnot

#2 02. 11. 2017 14:49 — Editoval Ferdish (02. 11. 2017 14:49)

Re: Obor Hodnot

#3 02. 11. 2017 14:55

Re: Obor Hodnot

#4 02. 11. 2017 15:00 — Editoval Ferdish (02. 11. 2017 15:01)

Re: Obor Hodnot

#5 02. 11. 2017 15:20

Re: Obor Hodnot

#6 02. 11. 2017 15:35

Re: Obor Hodnot

#7 02. 11. 2017 15:47

Re: Obor Hodnot

#8 02. 11. 2017 16:44

Re: Obor Hodnot

#9 02. 11. 2017 16:52

Re: Obor Hodnot

#10 02. 11. 2017 17:06

Re: Obor Hodnot

Zápatí