Matematické Fórum

Pavel · 01. 11. 2017 23:04

Určete integrál

$\boldsymbol{\int_0^1\int_0^1\{\frac xy\}\,\mathrm dy\,\mathrm dx}$

kde $\{z\}$ označuje zlomkovou část reálného čísla $z$ .

check_drummer · 04. 11. 2017 21:57

Ahoj,
co odečíst integrály x/y a celé části x/y? Ale je to jen výstřel od boku.

Xellos · 04. 11. 2017 23:05

↑ check_drummer:
Integral x/y diverguje, takze to velmi nepojde :D

Xellos · 05. 11. 2017 01:21

Fixnime $y$ . Nech $\lfloor 1/y \rfloor=n$ a $1-ny=z$ je desatinna cast. Potom
$\int_0^1 \left\lbrace\frac{x}{y}\right\rbrace \mathrm{d} x = n\int_0^y \frac{x}{y}\mathrm{d}x + \int_0^z \frac{x}{y}\mathrm{d}x=\frac{ny^2+z^2}{2y}\,.$
Potrebujeme teraz vyratat
$\int_0^1 \frac{n(y)y}{2}+\frac{z(y)^2}{2y}\mathrm{d}y = \frac{1}{2} \int_0^1 n(y)y+\frac{1}{y}+n(y)^2y-2n(y) \mathrm{d}y\,.$
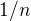Interval $y$ ktore maju dane $n$ je od $1/(n+1)$ po $1/n$ . Integral teda mozeme prepisat na
$\frac{1}{2} \sum_n \int_{1/(n+1)}^{1/n} ny+\frac{1}{y}+n^2y-2n \mathrm{d}y = \frac{1}{2} \sum_n n(n+1)\frac{1}{2n^2}-n(n+1)\frac{1}{2(n+1)^2}+\log \frac{n+1}{n} - 2n\frac{1}{n(n+1)}$
$= \frac{1}{2} \sum_n \frac{1-2n}{2n(n+1)} + \log\frac{n+1}{n}$
To sa uz dorata. S Wolframom mi vychadza $\frac{3-2\gamma}{4}$ , $\gamma$ je Euler-Mascheroniho konstanta.

Pavel · 08. 11. 2017 00:51

↑ Xellos:

1. Takže výraz $1-ny=z$ je desetinnou části čísla $1/y$ ? To nesedí.

2. Bylo by dobré dokončit celý příklad a ukázat, kde se ve výpočtu vzala konstanta $\gamma$ .

Xellos · 08. 11. 2017 11:26

Pavel napsal(a):
↑ Xellos:

1. Takže výraz $1-ny=z$ je desetinnou části čísla $1/y$ ? To nesedí.

To som vobec nepovedal. $z$ je zadefinovane ako $1-ny$ , tot vse; intuitivne som to nazval "desatinna cast", lebo ide o najmensie nezaporne cislo ktore dostaneme po opakovanom odcitani y od jednotky, co je analogicke definicii desatinnej casti (najmensie nezaporne cislo ktore dostaneme po opakovanom odcitani 1).

Pavel · 08. 11. 2017 22:33

↑ Xellos:

OK, už je to jasné. Postup je v pořádku, jen ten výsledek by bylo zapotřebí doladit.

Matematické Fórum

#1 01. 11. 2017 23:04

Integrál zlomkové části

#2 04. 11. 2017 21:57

Re: Integrál zlomkové části

#3 04. 11. 2017 23:05

Re: Integrál zlomkové části

#4 05. 11. 2017 01:21

Re: Integrál zlomkové části

#5 08. 11. 2017 00:51

Re: Integrál zlomkové části

#6 08. 11. 2017 11:26

Re: Integrál zlomkové části

Pavel napsal(a):

#7 08. 11. 2017 22:33

Re: Integrál zlomkové části

Zápatí