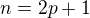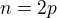Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 15. 11. 2017 19:11 Příspěvek uživatele check_drummer byl skryt uživatelem check_drummer. Důvod: Objevena chyba - 4. možnost je 023
#4 15. 11. 2017 19:18
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Binomial summation
↑ stuart clark:
Hi, is it 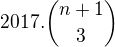 ? because i,j,k is number of 3 members sets in {0,..,n}
? because i,j,k is number of 3 members sets in {0,..,n}
"Máte úhel beta." "No to nemám."
Offline
#6 16. 11. 2017 09:13
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Binomial summation
Thanks ↑ check_drummer: and ↑ kerajs:
Offline



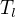 - trojúhelníkové číslo (triangular number)
- trojúhelníkové číslo (triangular number)