Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 11. 2017 17:35
Rozklad čtverce na několik čtverců
Ahoj.
Zjisti všechna n, pro která platí: `Čtverec lze beze zbytku rozdělit na  (ne nutně stejných) čtverců.'
(ne nutně stejných) čtverců.'
Rozdělením máme na mysli řezy rovnými čarami.
Popiš pro každé n konstrukci.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 17. 11. 2017 21:13 — Editoval vanok (17. 11. 2017 21:54)
Re: Rozklad čtverce na několik čtverců
Ahoj ↑ Darko:,
Hmm. Ja mam riesenie napr. na rozdelenie daneho stvorca napr. na 6;7;8 stvorcov.
( tie nie su take ako pises, cize su aj ine riesenia).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 17. 11. 2017 21:54
Re: Rozklad čtverce na několik čtverců
Pro začátek by bylo zajímavé dokázat, že obecné pravidlo, které ta všechna n musí splňovat, může existovat, nebo naopak dokázat, že takové pravidlo existovat nemůže.
Taky by bylo dobré upřesnit, zda ty dělící čáry vždy procházejí celým základním čtvercem, nebo můžou končit uvnitř.
Poznámka: Když si představím, s jak mizernými výsledky bádali matematici nad tzv. dokonalými čtverci, tak jsem dost skeptický k nějakému obecnému řešení.
Offline
#6 17. 11. 2017 22:08 — Editoval Darko (17. 11. 2017 22:39)
Re: Rozklad čtverce na několik čtverců
↑ vanok:
To si neumím představit. Můžeš uvést konkrétní příklad jak by jsi čtverec na takovýto počet rozdělil?
aka vyvrať moje tvrzení protipříkladem
Tady jsem vykreslil takový obrázek na hraní, je tam vidět jak to vyrýsovat (kromě dělení stran).
Je vidět:
// Všimni si, že když je ve čtverci jen 1 čára, musí být uprostřed, aby vznikly čtverce, jinak vzniknou i obdélníky.
// 2 čáry musíš dát do 1/3 a 2/3 strany, aby vznikly čtverce, atd...
- Strany musí být rovnoměrně rozděleny, aby vznikly čtverce.
- vznikne právě n^2 čtverců.
//jinak to nejde, nebo aspoň jinou variantu nevidím.
https://www.geogebra.org/m/ekf9FkTq
Offline
#7 17. 11. 2017 22:34 — Editoval vanok (17. 11. 2017 22:36)
Re: Rozklad čtverce na několik čtverců
↑ Darko:,
Napriklad na 7 stvorcov, rozdel stvorec na 4 casti tak aby ti to dalo 4 rovnake stvorce, a jeden zo 4roch stvorcov zasa na 4 casti
( tak, mas na koniec 4 « male » a 3 « velke » stvorce, cize do kopy 7). Ine ti necham hladat!
A nezabudni odpovedat na otazku od ↑ Andrejka3: !
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 17. 11. 2017 22:57
Re: Rozklad čtverce na několik čtverců
↑ Darko:,
No to je vec definicie.
V praktickom zivote ked sa kraja kolac, tak sa to robi vdaka useckam.
No pockajme ako to je myslene v ↑ Andrejka3:.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 18. 11. 2017 00:13
#12 18. 11. 2017 00:39 — Editoval edison (18. 11. 2017 01:06)
Re: Rozklad čtverce na několik čtverců
Nakonec je to vlastně jednoduché:
Nejmenší dělení je na 4, nevím zda jde 5, ale Vanok umí 6, 7, 8.
Protože každý čtverec lze rozdělit na 4, dá se jakékoli dělení zvyšovat o všechny celočíselné násobky 3.
Takže možná čísla jsou 4 + všechna přirozená čísla počínající 6, pokud má Vanok pravdu. Pokud ne, začíná to od 7.
Edit: Tak jsem na to ještě kouknul a ano, Vanok má pravdu, takže: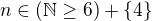
Offline
#13 18. 11. 2017 01:53 — Editoval Darko (18. 11. 2017 02:21)
Re: Rozklad čtverce na několik čtverců
↑ Andrejka3:
zjednodušení mě nenapadá..
z↑ edison:
menší oprava: Nejmenší dělení je 1, celý čtverec.
Offline
#14 18. 11. 2017 02:01
Re: Rozklad čtverce na několik čtverců
↑ Darko:
Rozdělme čtverec na 9 stejných dílů (3x3) a potom dejme tomu 4 čtverce počínaje levým dolním rohem spojme do jednoho. Dostaneme 1 velký a 5 malých, dohromady 6. Tvůj algoritmus je zjevně chybný, pokud to nepřipouští:-)
Offline
#15 18. 11. 2017 02:12 — Editoval edison (18. 11. 2017 02:15)
Re: Rozklad čtverce na několik čtverců
Takže abych to shrnul:
1. Každý čtverec můžeme rozdělit na 4 díly, tedy jsou všechny 4+3N
2.↑ edison: je popsán způsob, jak docílit 6 a tedy 6+3N
3. (1) dává jako druhý výsledek 4+3=7
4. Pokud uděláme totéž jako (2), ale s 4x4 a spojením 3x3, dostaneme 7+1=8, tedy 8+3N
Tím máme souvislou řadu 3 hodnot a jestliže ke každé z nich lze přičíst libovolné 3N, kde N je přirozené číslo, dostáváme všechna následující přirozená čísla. Tedy včetně 11, nebo třeba 12345678987654321.
Offline
#17 18. 11. 2017 02:25
Re: Rozklad čtverce na několik čtverců
Ještě poznámka: To dělení lze provádět i jinými způsoby, takže se dá očekávat, že čím vyšší číslo, tím větší počet způsobů, jak takového počtu dílů dosáhnout.
Např. 11 lze získat i takto:
Čtverec 6x6 vodorovně rozpůlíme, dolní půlku rozpůlíme na dva 3x3, nahoře uděláme pruh 3 čtverců 2x2 a zbylé místo mezi horní a dolní řadou vyplníme šesti 1x1. Celkem 2+3+6=11
Offline
#19 18. 11. 2017 14:29
Re: Rozklad čtverce na několik čtverců
↑ Andrejka3:,
Pozdravujem,
Ano to je dobry dokaz, a jasne, ze ho treba doplnit pre n=2;3;5.
Mohli by sme sa pytat vela vela dalsych veci.
Naprklad, pre ake n, existuju stvorce ktorych rozdelenie je vytvorene zo stvorcov roznych velkosti?
Poznamka.
Zda sa, ze tento problem sa objavil v knihe od Dudeney : Amusement in Mathematics, 1917 ( problem 173).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 18. 11. 2017 20:40 — Editoval Andrejka3 (18. 11. 2017 21:06)
Re: Rozklad čtverce na několik čtverců
↑ vanok:
Ahoj.
Úloha rozložit čtverec o straně n na několik čtverců, z nichž každý má stranu prvočíselné nebo jednotkové délky. Najít pro dané n minimální počet čtverců v rozkladu... Jsou otevřené problémy. A asi zůstanou, z podstaty věci (prvočísla).
Díky. Pěkná zábava.
What does a drowning number theorist say?
'log log log log ...'
Offline
#21 19. 11. 2017 18:27 — Editoval vanok (19. 11. 2017 18:29)
Re: Rozklad čtverce na několik čtverců
Ahoj ↑ edison:,
Vyssie si napisal
Poznámka: Když si představím, s jak mizernými výsledky bádali matematici nad tzv. dokonalými čtverci, tak jsem dost skeptický k nějakému obecnému řešení.
Co su to tie dokonale stvorce?
A o ake mizerne vysledky ide?
Mozes ma poucit?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 19. 11. 2017 22:40
Re: Rozklad čtverce na několik čtverců
vanok napsal(a):
Co su to tie dokonale stvorce?
Jedná se o čtverce rozdělené na menší čtverce, přičemž ale díly nesmí být stejně velké.
A o ake mizerne vysledky ide?
Mizerné výsledky jsou, že se to řešilo snad tisíce let, ale první byl objeven až r. 1938 (69 dílů), další 1948 (24 dílů) a pak 1978 (21 dílů, což má být nejmenší možný). O dalších nevím:-)
Offline
#23 19. 11. 2017 22:47
Re: Rozklad čtverce na několik čtverců
↑ edison:,
Dakujem. To som nevedel, ze sa to tak vola.
Miserne mozno, ale je tazko take najst.
V odkaze z #19 sa hovorilo iba o specialnom pripade stvorca z #1. Ale v tej knihe su aj ine hlavolamy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

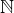 druhá odmocnina.
druhá odmocnina.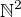 , pokud to interpretuji jako přirozená čísla umocněná na druhou, ne uspořádané dvojice z N.
, pokud to interpretuji jako přirozená čísla umocněná na druhou, ne uspořádané dvojice z N.