Matematické Fórum

VirtualPaws

Dobrý večer,
nevím si rady s následujícím příkladem, jde o to dokázat indukcí následující výraz

$\sum_{k=1}^n (-1)^{k+1}(\frac{k+2}{2})^2 = 3/4 + (-1)^{n+1}\frac{(n+2)(n+3)}{8}$

V základním kroku teda pro n=1 zjistím, že se obě strany rovnají
$L = (-1)^2(\frac{3}{2})^2 = 9/4$
$P = (-1)^2\frac{3*4}{8} = 9/4$

ale pak nevím jak se legalně zbavit těch sum v indukčním kroku...

misaH · 22. 11. 2017 21:52 — Editoval misaH (22. 11. 2017 21:54)

Len technická:

$P = (-1)^2\frac{3*4}{8} \ne 9/4$

Zabudol si na $\frac 34$

VirtualPaws · 22. 11. 2017 22:11

↑ misaH: Jo, špatně jsem to tu přepsal. Nicméně, kdyby aspoň někoho napadl jak postoupit o krok dál, budu rád.

KennyMcCormick

Teď dokážeš, že pokud platí rovnost pro $n$ , platí i pro $n+1$ .

$\left(\sum_{k=1}^n (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 = \frac34 + (-1)^{n+1}\frac{(n+2)(n+3)}{8}\right) \stackrel{?}{\Rightarrow}\nl \left(\sum_{k=1}^{n+1} (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 = \frac34 + (-1)^{n+2}\frac{(n+3)(n+4)}{8}\right)$ .

Pokud levá strana implikace neplatí, celá implikace jako celek platí.

Pokud levá strana implikace platí, pak levou stranu implikace můžeme odečíst od pravé strany implikace (je to ekvivalentní úprava, protože obě strany levé strany implikace se rovnají).

Po odečtení obou stran implikace získáš na levé straně $(n+1).$ člen sumy a na pravé straně rozdíl pravé strany pravé strany implikace a pravé strany levé strany implikace.

Po úpravách zjistíš, že rovnost platí.

Tudíž, platí-li levá strana implikace, platí i pravá strana implikace.

Tím je důkaz hotový. :)

Víš, jak dál?

VirtualPaws · 23. 11. 2017 00:26

Co znamená indukční krok tak nějak tuším, ale spíš si nevím rady s tou sumou... Pak mě napadá postupovat takhle, ale tady mě mate ta -1

$\sum_{k=1}^{n} (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 + (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 =$
$3/4 + (-1)^{n+1}\frac{(n+2)(n+3)}{8}+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2$
$3/4 + (-1)^{n+1}\frac{(n+2)(n+3)}{8}+ (-1)^{n+2}*\frac{n^2+6n + 9}{4}$

Darko · 23. 11. 2017 00:31

↑ VirtualPaws:
tu sumu můžeš odečíst od 3/4 a toho prvního zlomku .. viz předpoklad
a L=P

VirtualPaws · 23. 11. 2017 00:42

↑ Darko: asi nerozumím jak to myslíš

Darko · 23. 11. 2017 01:19 — Editoval Darko (23. 11. 2017 01:25)

↑ VirtualPaws:
předpoklad:
$\sum_{k=1}^n (-1)^{k+1}(\frac{k+2}{2})^2 = 3/4 + (-1)^{n+1}\frac{(n+2)(n+3)}{8}$

pro n+1:
$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}+(-1)^{n+2}\frac{(n+3)(n+4)}{8}$

$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}- (-1)^{n+1}\frac{(n+3)(n+4)}{8}$

$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}- (-1)^{n+1}\frac{n^{2}+7n+12}{8}$

$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}+(-1)^{n+1}\frac{-n^{2}-7n-12}{8}$

$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}+(-1)^{n+1}\frac{n^{2}+5n+6-2n^{2}-12n-18}{8}$

$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}+(-1)^{n+1}\frac{n^{2}+5n+6}{8}+(-1)^{n+1}\frac{-2n^{2}-12n-18}{8}$

$\sum_{k=1}^{n}[ (-1)^{k+1}\left(\frac{k+2}{2}\right)^2 ]+ (-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = \frac{3}{4}+(-1)^{n+1}\frac{(n+2)(n+3)}{8}+(-1)^{n+1}\frac{-2n^{2}-12n-18}{8}$

Úprava ekvivalentní s předpokladem:
$(-1)^{n+2}*\left(\frac{n+3}{2}\right)^2 = (-1)^{n+1}\frac{-2n^{2}-12n-18}{8}$

$(-1)^{n+1}*\left(\frac{-n^{2}-6n-9}{4}\right) = (-1)^{n+1}\frac{-2n^{2}-12n-18}{8}$

Vydělím (-1)^(n+1)

$\left(\frac{-n^{2}-6n-9}{4}\right) = \frac{-2n^{2}-12n-18}{8}$

/*8

$-2n^{2}-12n-18 =-2n^{2}-12n-18$

$0 = 0$

$L = P$

$QED$

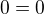
rip můj spánek :P