Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 27. 11. 2017 11:20 — Editoval vlado_bb (27. 11. 2017 11:21)
Re: Zápis exponentu
↑ MarST:Rovnost 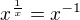 nastava iba ak
nastava iba ak 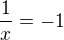 , teda ak
, teda ak 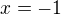 . Tu ale treba zvazit, co vlastne rozumieme pod zapisom
. Tu ale treba zvazit, co vlastne rozumieme pod zapisom  , cim sa zaoberalo ine vlakno pred par dnami - http://forum.matweb.cz/viewtopic.php?id=99528.
, cim sa zaoberalo ine vlakno pred par dnami - http://forum.matweb.cz/viewtopic.php?id=99528.
Offline

![kopírovat do textarea $x^{1/x}=\sqrt[x]{x} \ \ \ \wedge x\in \mathbb{N}_+$](/mathtex/97/971d3cf1a8e3b12ef6751f78479ffda8.gif)
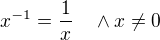
 ?
?