Matematické Fórum

Akraell

Zdravím,
možná jsem zase špatně násobil a sčítal...

Hornerovo schéma:
1 9 2 10 -67 45 (zvoleno číslo 1)
| 1 10 12 22 -45
-------------------
1 10 12 22 -45 0 (zvoleno číslo 1)
| 1 11 23 45
-------------------
1 11 23 45 0 (nyní žádné číslo nepasuje)

zbývá kubický polynom 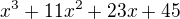$x^{3} + 11x^{2} + 23x + 45$
Rozhodl jsem se použít derivaci: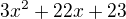
$3x^{2} + 22x + 23$
při součtu dvou kořenů kvadratické rovnice a po jejím dělením dvěma jsem získal číslo -11/3.
V této x-ové souřadnici by se podle mého chápání měl v kubické rovnici objevit kořen.
Podle Hornerova schématu to ale nesedí.

To hledání kořenů a extrémů pomocí derivací jsem ještě zkoušel na jednom příkladě.
Máme kubický polynom 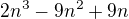$2n^{3} - 9n^{2} + 9n$
její kořeny jsou 0, 1.5 a 3.
první podezření z extrému: (0+1.5)/2 = 0.75
druhé podezření z extrému: (1.5+3)/2 = 2.25

0.75 zní dobře, ale je to špatný výsledek.
Když ten polynom zderivuji a použiji znova ten postup, pak vyjde 0,634... a to je zrovna správný výsledek

Matematické Fórum

#1 11. 12. 2017 19:36 — Editoval Akraell (11. 12. 2017 19:37)

Hornerovo schéma a otázka k hledání extrému

Zápatí