Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 05. 2009 20:31
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Kolmost rovin
Že jejich normálové vektory jsou také kolmé (skalární součin roven nule).
Offline
#5 16. 05. 2009 20:42
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Kolmost rovin
Ne, jen tečkou. x se značí vektorový.
Skalární je 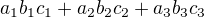
Offline
#7 16. 05. 2009 21:05
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Kolmost rovin
↑ muminekxx:
No a co máme počítat? Libovolnou kolmou rovinu? Nebo co?
Offline
#9 16. 05. 2009 22:12
- marnes

- Příspěvky: 11227
Re: Kolmost rovin
↑ muminekxx:Mohou. Třeba si představ krychli a přední stěna(rovina) je kolmá k boční stěně(rovině). A dvě roviny nemohou mít průsečík, ale průsečníci - přímku. U té krychle je to hrana.
Jo. A na začátku vás zdravím.
Offline