Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 05. 2009 12:38
- k.niccy@seznam.cz
- Příspěvky: 144
- Reputace: 0
Logaritmická rovnice
Ahoj,nějak jsem se v závěru zasekla:
Offline
#3 16. 05. 2009 13:15
- k.niccy@seznam.cz
- Příspěvky: 144
- Reputace: 0
Re: Logaritmická rovnice
Aha,děkuji
Můžu ještě poprosit otento?
když použiju substituci,dostávám se kněčemu podobnému jako v tom předchozím
Offline
#6 16. 05. 2009 13:37
Offline
#7 16. 05. 2009 13:39 — Editoval svatý halogan (16. 05. 2009 13:41)
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Logaritmická rovnice
↑ ttopi:
Spokojen :)
Edit: i když z formálního hlediska... když na levé straně máš 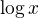 , tak se očekává jedna hodnota vpravo. Je to něco jiného, když máš třeba
, tak se očekává jedna hodnota vpravo. Je to něco jiného, když máš třeba  . Takže formálně je lepší asi
. Takže formálně je lepší asi 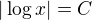 a nevím, zda
a nevím, zda  je vůbec správně a zajímalo by mne, jak to tedy je.
je vůbec správně a zajímalo by mne, jak to tedy je.
Počkáme si na Mariana/Pavla/Pavla.
Offline
#8 16. 05. 2009 13:44
Re: Logaritmická rovnice
↑ svatý halogan:
Samozřejmě, že správně by měla být ta absolutní hodnota. Nebo třeba taky  , ne?
, ne?
Ve vzorci pro výpočet kořenů kvadratické rovnice se taky vyskytuje 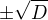 tak proč ne tady :-)
tak proč ne tady :-)
oo^0 = 1
Offline
#9 16. 05. 2009 13:55
- k.niccy@seznam.cz
- Příspěvky: 144
- Reputace: 0
Re: Logaritmická rovnice
Dle výsledků,je to správně,děkuji mnohokrát!
Offline
#10 16. 05. 2009 14:13
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Logaritmická rovnice
↑ ttopi:
Ve vzorci pro výpočet kořenů je ale vstupem množina dvou bodů - x_{1, 2}, proto mohu mít \pm na druhé straně.
Nechci být nějaký pedant, jen mě zajímá korektní zápis.
Offline
#11 16. 05. 2009 21:47
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
muzete mi nekdo vysvetlit jaktože u tehoto logaritmu 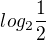 vyjde vysledek -1
vyjde vysledek -1
Offline
#12 16. 05. 2009 21:52 — Editoval marnes (16. 05. 2009 21:52)
- marnes

- Příspěvky: 11227
Re: Logaritmická rovnice
↑ vonSternberk: a teď se ptáš 2^x=1/2 a to je pro -1
a teď se ptáš 2^x=1/2 a to je pro -1
1/2 je dvě na -1
Jo. A na začátku vás zdravím.
Offline
#13 16. 05. 2009 22:01
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
no mám zadanej příklad:
vypočítej hodnoty 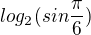 ..sin 30° je 0,5 a tak mi vyslo
..sin 30° je 0,5 a tak mi vyslo 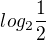 , ale s timto uz jsem si nevedel rady:( a ve vysledku je, že ma vyjit -1
, ale s timto uz jsem si nevedel rady:( a ve vysledku je, že ma vyjit -1
Offline
#14 16. 05. 2009 22:09
- marnes

- Příspěvky: 11227
Re: Logaritmická rovnice
↑ vonSternberk:
Tak třeba log(2)8=3 protože 2 na 3 je 8
log(2)32=5 2 na 5 je 32
log(2) 1/2=-1 2 na -1 je 1/2
Jo. A na začátku vás zdravím.
Offline
#15 16. 05. 2009 22:15
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
↑ marnes: nechapu to...jak, ale prijdu na to, že -1?
Offline
#16 16. 05. 2009 22:22
- marnes

- Příspěvky: 11227
Re: Logaritmická rovnice
↑ vonSternberk:
log(a)x=y právě když a na y = x to je definice logaritmu (a) je základ
log(2)1/2=y 2 na -1= 1/2
Jo. A na začátku vás zdravím.
Offline
#17 16. 05. 2009 22:30
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
jo to znamená, že 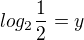 ...
... ...
...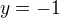 ...je to tak?
...je to tak?
Offline
#18 16. 05. 2009 22:39
- marnes

- Příspěvky: 11227
Re: Logaritmická rovnice
↑ vonSternberk:Ne 2y ale 2 na y=1/2!!! 2 na prvou je dva a dva na mínus prvou je 1/2. Třeba 3na-1je 1/3, 4na-1je 1/4, atd
Jo. A na začátku vás zdravím.
Offline
#19 17. 05. 2009 10:53
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
jasný...takže  ...
... ...
...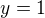 ...ale vyjit má -1...kde jsem udělal chybu?
...ale vyjit má -1...kde jsem udělal chybu?
Offline
#20 17. 05. 2009 12:14 — Editoval marnes (17. 05. 2009 12:53)
- marnes

- Příspěvky: 11227
Re: Logaritmická rovnice
↑ vonSternberk:Nenenenenenene. Ty mi dáváš:-)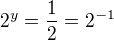 a z toho y = -1 Hlavně netvrď, že se tou 2 dělí!! To je exponenciální rovnice, převedená na základ 2 a potom se vytváří rovnice jen z exponentů!!
a z toho y = -1 Hlavně netvrď, že se tou 2 dělí!! To je exponenciální rovnice, převedená na základ 2 a potom se vytváří rovnice jen z exponentů!!
Jo. A na začátku vás zdravím.
Offline
#21 18. 05. 2009 08:49
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
↑ marnes: díky (především za trpělivost):)
Offline
#23 18. 05. 2009 14:48 — Editoval Marian (18. 05. 2009 14:48)
Re: Logaritmická rovnice
Offline
#24 18. 05. 2009 14:53
#25 18. 05. 2009 14:55
Re: Logaritmická rovnice
↑ marnes:
Nebylo by jednodušší naučit se zapisovat matematiku v TeXu (nebo v jeho editoru zde přítomném), než sem dávat foto nebo skenovaný obrázek? Čistě nenásilný návrh technického charakteru s estetickými důsledky ...
Offline

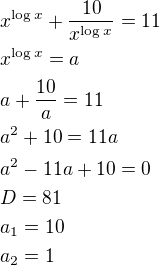
 a
a 

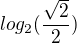 jak to bude?
jak to bude?
