Matematické Fórum

Akraell

Zdravím,

Příklad:
arctg(-3 / (x^2 - 1)) Najděte body nespojitosti a určete typ.

1. Funkce je spojitá na celém definičním oboru D(f)
-s tímhle nejsou problémy

2. body nespojitosti jsou -1, 1
-to také není těžké

3. 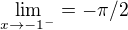$\lim_{x\to-1^{-}} = -\pi /2$ a zprava je hodnota kladná
-To už je pro mě těžký problém. Vůbec nevím, kde se vzala pí půl.
Jediná možnost, která mě napadá je vědět, jaký je společný nejomezenější maximum a minimum. Což je právě pípůl z funkce arctg.

Další příklad:
x/sin(x)
-Zde mám trochu problém se sin(x). Myslím, že sin(pí/2) bude 1 a výsledek ze zlomku bude pí/2. Graf tedy bude podle mě zvětšující sinusoida, protože x je rostoucí přímka. Ale vůbec nevím, co se v okolí nuly děje. Nejomezenější je funkce sinus se skokem 2 (|-1| + 1). Jelikož je x silnější než sin(x), tak mě napadá, že to bud mít v nule odstranitelnou nespojitost. Ale zvětšující sinusoida to nebude, problém je, když jmenovatel bude 0, tak se bude něco dít a to se děje periodicky. Možná se bude jednat o neodstranitelnou nespojitost 1. řádu se skokem 2. Postupně se bude ten skok možná zvětšovat. Jenže realita je jiná. Ve všech nulových hodnotách sin(x) je NN2Ř.

Je tu mnoho dalších případů (asi skoro všechny), kdy nemám šanci určit správný výsledek.
Prosím o radu.

LukasM · 30. 12. 2017 23:54

↑ Akraell:
U toho prvního bych začal s limitou argumentu funkce arctg. Výpočet limity 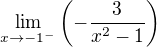$\lim_{x\rightarrow -1^{-}}{\left(-\frac{3}{x^2-1}\right)}$ snad nebude dělat problémy. Limita čitatele je konečná a kladná, jmenovatel se při přibližování k -1 zleva blíží nule zprava, takže limita zlomku je $+\infty$ . A protože je před ním mínus, argument jde k $-\infty$ . Počítáme tedy (arctg je spojitá funkce) $\lim_{x\rightarrow -\infty}{ \left(\mathrm{arctg}{\ x}\right)}=-\frac{\pi}{2}$ .

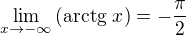U té dvojky absolutně nerozumím tvým úvahám. Je pravda, že v nule je odstranitelná nespojitost, funkci stačí dodefinovat jedničkou. Ve všech ostatních bodech, kde 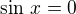$\mathrm{sin}{\ x}=0$ se musíš zamyslet nad hodnotou (a existencí) limit zleva a zprava. Argumentace bude podobná jako výše, limity budou nevlastní a opačného znaménka. Graf funkce viz Wolfram.

Akraell · 31. 12. 2017 15:22

Asi je problém právě v těch limit.
Když vidím tu limitu a v ní x->-1, tak je asi nutné do toho x^2 dosadit -1. Ani při úpravách toho zlomku se nemohu dostat z pasti.
Nedokážu pochopit "jmenovatel se při přibližování k -1 zleva blíží k nule zprava". Jisté je ale to, že je v tom zlomku krásně vidět hyperbola a v těch bodech nespojitosti se projeví nevlastní limita.

Zkrátka, přijde mi, že mi počítání nepomůže, žádný počítání v tomhle neexistuje. Protože všude v zadáních a řešeních vidím limitu, která se nedá vypočítat, za ní magický výsledek a pár grafů okolo, na kterých jsou vidět důkazy.
Takže mi připadá, že musím jen dokázat v každých funkcí vidět jak vypadá graf a podle toho napsat výsledky. Jenže to mi vůbec nejde.

Teď jsem ale pochopil, že když bude problém uzavřený např. v sin(problém) a bude to mít vlastnosti hyperboly, tak díky funkce sinus bude obor hodnot omezený na <-1,1> a tím pádem to bude neodstranitelná nespojitost 1. řádu se skokem 2.

Matematické Fórum

#1 30. 12. 2017 22:56 — Editoval Akraell (30. 12. 2017 22:57)

Vyšetření body nespojitosti

#2 30. 12. 2017 23:54

Re: Vyšetření body nespojitosti

#3 31. 12. 2017 15:22

Re: Vyšetření body nespojitosti

Zápatí