Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezení středu v kuželosešce (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 01. 2018 11:40
Nalezení středu v kuželosešce
Dobrý den, mám problém vypočítat souřadnice středu v původní soustavě souřadnic. Výpočet převedení na kanonický tvar včetně posunutí a translace jsem pochopila. Nyní mám úkol převést nové souřadnice středu na staré. Tedy z S" (nové) na S' (posunutí) a poté na S (díky rotaci; staré).
Nový střed má souřadnice S[0,0].
Ty jsem poté dosadila do rovnic: 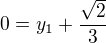
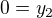
Z nich jsem dostala ![kopírovat do textarea $S'[\frac{-\sqrt{2}}{3},0]$](/mathtex/bc/bcbb1efe33b0280d89706f68bb353cc9.gif)
Nyní přichází problém, jak zjistit S v původní soustavě díky rotaci. Vím, že bych měla dosadit do rovnic 4.25. Ve výsledcích je [-1/3; -1/3]. Pokud dosadím za y1 a y2 souřadnice S', tak mi ale vyjde jiný výsledek. Dosazuji tedy špatně?
Tento příklad byl vzat z materiálu Geometrie 1 - Miroslav Lávička
Offline
- (téma jako vyřešené označil(a) Johana16)
#2 04. 01. 2018 11:59
Re: Nalezení středu v kuželosešce
↑ Johana16:
A obdobně bych se chtěla zeptat i na osy
v nové mají
x"=0 a y"=0
Ty dosadím podobně jako S" do rovnic a vyjde mi: 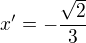 a y'=0
a y'=0
Dál netuším jak.
Offline
#3 04. 01. 2018 13:17 — Editoval Jj (04. 01. 2018 13:20)
Re: Nalezení středu v kuželosešce
↑ Johana16:
Zdravím.
Řekl bych, rotujte o úhel  .
.
Pokud se tedy nemýlím.
Offline
#5 04. 01. 2018 19:52 — Editoval Jj (04. 01. 2018 19:58) Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: zřejmě chyby
#6 04. 01. 2018 20:57 — Editoval Jj (04. 01. 2018 21:07)
Re: Nalezení středu v kuželosešce
↑ Johana16:
Střed kuželosečky má v soustavě S'' souřadnice (0,0).
Pokud je soustava S'' vůči soustavě S' posunuta o (m,n), pak má střed kuželosečky v S' souřadnice (m,n):
x'' = x' - m ---> x' = x'' + m = 0 + m = m
y'' = y' - n ---> y' = y'' + n = 0 + n = n
Pokud je soustava S' vůči soustavě S otočená o úhel  , pak má střed kuželosečky v soustavě S, otočené vúči S' o úhel
, pak má střed kuželosečky v soustavě S, otočené vúči S' o úhel  , souřadnice
, souřadnice
Konkrétněji neporadím - ve výpisu výpočtu ne vše vidím a ne všemu rozumím.
Edit - doplněno:
Nebo do soustavy 4.25 dosadit (m,n) za (x1, x2) a spočítat (y1, y2), což by zřejmě mělo vést k témuž výsledku.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezení středu v kuželosešce (TOTO TÉMA JE VYŘEŠENÉ)

