Matematické Fórum

Johana16 · 07. 01. 2018 17:20

Dobrý den, prosím o radu s výpočtem integrálu: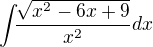

$\int_{}\frac{\sqrt{x^2-6x+9}}{x^2}dx$
čitatel zlomku jsem si převedla na (x-3)^2 odmocninu jsem díky mocnině zrušila a ve zlomku mi zbylo (x-3)/x^2.
Po vypočtení jsem dostala 3/x. Ve výsledcích je však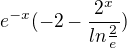
$e^{-x}(-2-\frac{2^x}{ln\frac{2}{e}})$
Poradíte mi prosím, jak tedy počítat správně?
Děkuji

kerajs · 07. 01. 2018 18:38

$\int_{}\frac{\sqrt{x^2-6x+9}}{x^2}dx=\int_{}\frac{|x-3|}{x^2}dx=sgn(x-3)\cdot (\ln |x|+\frac{3}{x})+C$

misaH · 07. 01. 2018 18:52

↑ Johana16:

Ahoj :-)

Technická:

$\int_{}\frac{\sqrt{x^2-6x+9}}{x^2}dx=\int_{}\frac{|x-3|}{x^2}dx=sgn(x-3)\cdot $\ln |x|+\frac{3}{x}$+C$

$\int_{}\frac{\sqrt{x^2-6x+9}}{x^2}dx=\int_{}\frac{|x-3|}{x^2}dx=sgn(x-3)\cdot
$\ln |x|+\frac{3}{x}$+C$

Matematické Fórum

#1 07. 01. 2018 17:20

Výpočet integrálu

#2 07. 01. 2018 18:38

Re: Výpočet integrálu

#3 07. 01. 2018 18:52

Re: Výpočet integrálu

Zápatí