Matematické Fórum

↑ Akraell:
Zdravím, podle mě není dána funkce prostá, tudíž nemůže mít inverzní funkci. :)

Poznamka. ( I ked viaceri ludia tu hovoria bludy o inverznych funkciach, dam tu tento text, ktory moze pomoct, presnejsie som pisal o tomto pojme v sekcii diaktika)
Otazka je spatne polozena.( dam tu schematicky moznu odpoved)
Asi treba najt restrikcie funkcie na maximalnych podmnozinach na ktorych inverzna funkcia existuje. 
Ak vysetrime povodnu funkciu 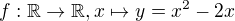, tak lahko uvidime, ze ide o spojitu funkciu, ktorej graf je parabola vrcholu 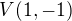a ktora je monotonna na kazdom z intervalov a jej obraz je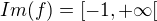

Tak z danej povodnej funkcie mozme uvazovat dve restrikcie ktore maju inverznu funkciu
Jedna z nich je ( druhu necham na doplnenie )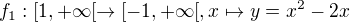

( ako vidite ide o bijekciu, co je nutna a postacujuca podmienka aby inverzna funkcia existovala!)
Ta sa vyjadri takto
( poznamenajte, ze grafy funkcii 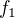a 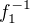su symetricke vzladom k priamke «  prva osa » rovnice 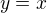v orhonormalom repere roviny.

Děkuji za odpovědi.
Omlouvám se za špatně položené zadání. Chybí tam 
Chtěl jsem jen vyjádřit z rovnice x a pak výsledek omezit o restrikci. Napadlo mě pro vyjádření x odmocnit obě strany, ale s tímto postupem  neumím pracovat: 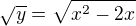Asi v té druhé straně bude obdoba známého vzorečku, ale nejsem si jist, jak by to vyšlo, možná něco jako 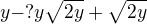a ani si nejsem jist, jestli by mi to pomohlo.

Přímo s bijekcí jsem ještě tak aktivně nepracoval. Ale mám v sešitě z jednoho předmětu napsáno:
L([a;b]) = [a - b; 3a + 2b]^T


-----------------



Určit inverzní matici mi nedělá problém. Ale inverzní matici k y = x^2 + x už asi nepůjde určit. 

Zatím tedy v té bijekci nevidím, jak postupovat k tomu výsledku.

↑ vlado_bb:,
Pozdravujem. 
No moj dokaz nie je uplny.  Treba doplnit dokazy vsetkych mojych afitmacii. 
Cize som dal pekny navod.   No jeho odkopirovanie nestaci. To je nedostatocne....

↑ vanok:
Protože jsem středoškolák a ne z gymnázia. Alespoň jsem určitě nebyl v tak dobré střední škole. S touhle rovností se setkávám poprvé a nedivím se, že je mezi "středoškoláky" oblíbená, taky se mi hned zalíbila. Na střední jsme se jen učily  počítat "pod-základní vzorečky a počítání" a pouze tak mechanicky, že jsem se nenaučil při počítání přemýšlet.
Děkuji za její ukázku.



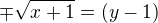
pro druhou restrikci je to tedy:


To, že se mi objevilo před odmocninou 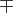by mi řeklo, že máme 2 restrikce a podle toho bych pak ještě dořešil, která restrikce to je. Tímto způsobem jsem řešil úlohy, které chtějí pouze najít inverzní funkci, aniž bych věděl o definičním oboru, monotonnosti atd. Pak bych řešil, jaká jsou pravidla rovnosti funkcí jako např. e^x = ln|x|.


Ten návod byla příznivější metoda, kdy se vlastně musí pořádně vyšetřit, jak se funkce zobrazí v grafu, jak je posunutá v ose x, zrychlená atd a podle toho zobrazit, posunout, zrychlit.... inverzní funkci. Pochopil jsem správně?

Děkuji moc

Pozdravujem, pre istotu doplnim tu tebou  uvazovanu restrikciu, ktory oznacim 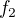a jej inverznu funkciu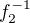
( analogicky ako tu ↑ vanok:)

Skrytý text:




(restrikcia je bijektivna)