Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 01. 2018 14:24
Věta o existenci extrémů (důkaz)
Zdravím, chápu první část důkazu, kde se dokazuje maximum funkce pomocí věty o supremu (svazuje supremum a limitu posloupnosti):
máme posloupnost yn z nějaké množiny funkčních hodnot M (je omezená), pak xn (dle Bolzano-Weierstrassovy věty, že z každé omezené posloupnosti lze vybrat konvergentní posloupnost) z intervalu a, b (uzavřený), kde je fce definována.
Xn se limitně blíží k nějakému bodu, např. c z intervalu a, b (uzavřený), funkční hodnota v tomto bodě je naše supremum, zvoleno jako G a protože limita posloupnosti xn je náš bod c a limita v bodě c je G, tak G je supremum, tedy maximum fce.
V druhé části dokazujeme minimum fce. Volíme si g(x)=-f(x). Pak nerozumím následujícím tvrzení:
g je na intervalu a,b (uzavřený) spojitá a tedy nabývá na a,b svého maxima podle již dokázané věty.
Nechť tomu tak je v bodě x* pak platí  kdykoliv x je z intervalu a, b (uzavřený).
kdykoliv x je z intervalu a, b (uzavřený).
To znamená, že 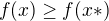 pro každé x z intervalu a,b (uzavřený) a f nabývá svého minima na a,b (uzavřený) v bodě x*.
pro každé x z intervalu a,b (uzavřený) a f nabývá svého minima na a,b (uzavřený) v bodě x*.
Jak může fce g nabývat svého maxima podle první části věty, když má předpis jaký má? Nemělo by v bodě, kde je maximum g, být spíše minimum vzhledem k předpisu?
Offline
#2 12. 01. 2018 11:06
Re: Věta o existenci extrémů (důkaz)
Už je mi to jasné, nejdříve v druhé části ukážeme, že naše hledání maxima pro f můžeme uplatnit pro g.
Tedy g je všude menší maximum v nějakém dalším x. Pak f je všude větší než v bodě maxima g a pak máme i minimum f.
↑ m.sey:
Offline
