Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 05. 2009 19:11
Re: globální a lokální extrémy
Zadání není kompletní, 100cm obvod čeho?
Při jednom počítáš lokální maximum a při druhém lokální minimum (dá se to zjistit podle znaménka druhé derivace v bodě extrému), ale pokud se nad tím zamyslíš, tak někdy bývá buď minimální nebo maximální objem v daném případě nesmysl.
Don't waste your time, or time will waste you.
Offline
#3 17. 05. 2009 19:28
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: globální a lokální extrémy
Něčeho obvod a počítáš jeho objem? Obsah tedy?
A jak říká kolega ↑ Blizzy:, jde o to, zda počítáš objem či povrch. U objemu (snad) dává smysl pouze maximální objem (při daném povrchu). U daného objemu hledáme minimální povrch.
Většinou se dostaneme k parabole, která nám dá jen jeden extrém.
Offline
#4 17. 05. 2009 22:06
Re: globální a lokální extrémy
↑ svatý halogan:
ahoj, mame zadání. Obvod pravoúhleníku ma 100cm. Urcete nejvetsi objem.
Mame Objem pravouhlenik 625cm2 a urcete minimalni povrch..
MOhli byste mi to prosím pomoct vypocitat..Ja to vubec nechapu.
Offline
#5 18. 05. 2009 00:08 — Editoval O.o (18. 05. 2009 00:15)
Re: globální a lokální extrémy
↑ muminekxx:
Ahoj -),
mne se tyhle úlohy strašně líbí, ale nejsem si vůbec jistý, jestli bych to udělal správně, tak zkusím jen něco plácnout v tuhle hodinu a když to nepůjde, tak to verte, jako že můj mozek již nepracoval ;-).
Takhle to asi nepůjde, připadalo by mi to moc jednoduché. Někde bude háček velikost nákladního vagonu..
Offline
#6 18. 05. 2009 00:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: globální a lokální extrémy
↑ O.o:
Zdravím :-)
kyselinu draselnou bys neuměl?
------------------
↑ muminekxx:
máš tam vážně velký zmatek v zadání (kolega O.o to jistě za chvilku - nebo zítra vysvětlí, co ho tak neskutečně zmatlo - a už vysvětluje, jak vidim z náhledu) - jinak pro postup podobných uloh: http://www.mojeskola.cz/Vyuka/Php/Learn … rokem5.php
Offline
#7 18. 05. 2009 00:28 — Editoval O.o (18. 05. 2009 00:31)
Re: globální a lokální extrémy
↑ jelena:
Také zdravím -),
kyselinu draselnou bych už dnes asi nezvládl, ale daří se mi občas jiné věci, jako, například výše, nějak jsem si neuvědomil, že když se chce objem, půjde o nějaký třetí rozměr (ani nevím, nějak jsem si říkal, že k obvodu se bude hodit obsah a dále jsem to už moc nepročítal), tak to mé je celé špatně, ruším to, nikdo se na to raději nekoukejte ;-).
PS: Teď řeším spíš adice u organických záležitostí, ty jsou mi naštěstí daleko sympatičtější, tak ani nestrádám a učím se rád, jen potřebuji umět celá skripta v úterý ráno (včetně výpočtů do chemie .() a zatím jsem ve fázi zvýrazňování důležitých partií, tak to nevidím ještě úplně růžově.. ^.^
Offline
#9 18. 05. 2009 07:18
Re: globální a lokální extrémy
prosim, nezkusil bys vypocitat to s tim obsahem 625cm2, me to vychazi uplne divne. Vysledek po prvni derivaci 24,5cm a ruha derivace mi vychazi dlouhy polynom děleno b4 .. takze pak dosadim do druhe derivace 24,5cm a kdyz mi to vyjde vetsi nez O - je to lok.minimum?
Offline
#10 18. 05. 2009 07:28 — Editoval Cheop (18. 05. 2009 07:33)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: globální a lokální extrémy
muminekxx napsal(a):
↑ svatý halogan:
ahoj, mame zadání. Obvod pravoúhleníku ma 100cm. Urcete nejvetsi objem.
Mame Objem pravouhlenik 625cm2 a urcete minimalni povrch..
MOhli byste mi to prosím pomoct vypocitat..Ja to vubec nechapu.
V zadání píšeš, že máme objem pravoúhelníku 625 cm^2, což je nesmysl, protože objem tělesa se udává v cm^3.
Napiš sem prosím pořádné zadání.
Tak jak jsi ho napsal Ty je to zadání určitě špatně.
Nevím tottiž co počítat.
Originální zadání příkladu zní zcela určitě jinak (tak sem s ním)
Nikdo není dokonalý
Offline
#12 18. 05. 2009 08:42 — Editoval Cheop (18. 05. 2009 08:46)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: globální a lokální extrémy
↑ muminekxx:
Strany pravoúhelníku a,b pak musí platit: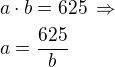
 rovnici derivujeme dle b a derivaci položíme rovnu nule
rovnici derivujeme dle b a derivaci položíme rovnu nule![kopírovat do textarea $\left[2\left(\frac{625+b^2}{b}\right)\right]^'=0\nl-\frac{625}{b^2}+1=0\nlb^2=625\nlb=25$](/mathtex/94/945b496b39ca8d77b4b682d5dc236d24.gif) dopočítáme druhý rozměr
dopočítáme druhý rozměr
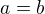 jedná se o čtverec
jedná se o čtverec
Když to bude čtverec, tak obvod pravoúhelníku bude minimální.
Nikdo není dokonalý
Offline