Matematické Fórum

Zvedavec 4

V techto dvou prikladech na wiki https://en.wikibooks.org/wiki/Special_Relativity v casti "Spacetime" v trochu min nez polovine stranky je bud chyba, coz se muze stat, anebo jsou predstaveny z rozdilneho pohledu, coz by tedy dost pletlo.

Jestlize 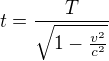$t=\frac{T}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ jak se tam udava, nemelo by potom obdobne, x byt 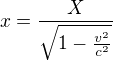$x=\frac{X}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ ? To znamena, ze jestlize Johnovo t ukaze t>T, pak by snad i jeho x melo ukazat, ze x>X. Aby se to cele nepletlo, nemela by velka pismena oznacovat jednu soustavu a mala tu druhou?

Jinak muzou mit na mysli, ze tedy kdyz John uvidi ze sve planety, ze Billovy hodinky ukazi T=1 vterina, pri pohledu na sve uvidi, ze t bude vic nez 1 vterina.

A potom jestlize Bill nameri delku sve tyce coby X, kdyby ji byl schopen zmerit John a stat pritom na sve planete, nenameril by jeji delku coby x, tedy vetsi nez X ????

Je mi jasne, ze jde o to, ze se cas "zdilatuje" a delka tyce "zkontraktuje" v soustave "v pohybu" vuci casu a delce v soustave "v klidu".

Ale zda se, ze to tady maji hrozne pomotany, takze se v tom da jenom tezko vyznat, co maji na mysli.

Protoze v prvnim priklade nazyvaji male t coby cas souradny, ktery je vetsi (vic vterin) nez velke T , tedy cas vlastni a ve druhem nazyvaji sice male x taky souradnou delkou, ale tvrdi, ze je mensi nez velke X, tedy vlastni delka. Nemely by T spolu s X patrit do jedne ze soustav a t spolu s x patrit do te druhe?

Takze na konci tvrdi, ze $T=\frac{v}{c^{2}}X$ . I kdyz ten vysledek odpovida pocetnimu postupu co mu predchazi, nevim jestli se tomu da verit, protoze bych si myslel, ze by ten vzorecek mel porovnavat ty dve soustavy a tedy bud namisto T by v nem melo byt t anebo namisto X by v nem melo byt x. Protoze snad T patri do soustavy spolu s X a t do stejne soustavy co x?

Mohl by to nekdo okomentovat?

Zvedavec 4

Kdyz tedy prijmu cas T, coby vlastni cas hodin posuzovany z jejich vlastni soustavy, tedy soustavy "v klidu" a cas t, coby cas jiny nez T, a znaceny coby cas souradny, bude tedy ten souradny cas t muset byt casem T, ale posuzovanym z te druhe soustavy, tedy ze soustavy "v pohybu".

Pak by tedy vztah mezi temi dvema casy mel byt, ze T>t.

Zda se jasne, ze to je cele hodne zvadejici a da se o tom tezko diskutovat.

Protoze casem T se tady mysli Billuv cas jak posuzovany Billem samotnym, casem t se mysli Billuv cas, jak posuzovany Johnem, ktery ho srovnava se svym vlastnim casem T a mel by tedy, podle STR usoudit, ze ten Billuv cas T, videny Johnem coby t, by mel byt mensi=pomalejsi=zdilatovany oproti Johnovu vlastnimu casu T. Tedy John by si taky mel myslet, ze T>t.

Ze vzorecku 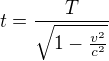$t=\frac{T}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ se ale zda vyplivat pravy opak, jestli se tu nepletu, ze t>T i kdyz casem t se zase mysli Billuv cas T jak videny Johnem. Takze se tu jevi zdanlivy nesoulad.

Jelikoz ze vzorece 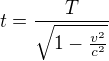$t=\frac{T}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ se zda vyplivat, ze t>T a z jejich dalsiho vzorce 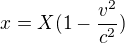$x=X(1-\frac{v^{2}}{c^{2}})$ , jestli to nemaji spatne, by pak naopak vyplivalo, ze x<X, ty dva vzorecky se tedy taky zdaji byt v nesouladu.

Byl bych rad, kdyby se tedy mohl nekdo vyjadrit alespon k tomu druhemu nesouladu mezi t a x, tedy jestli to, ze ty dva vzorce jsou ve zdanlivem nesouladu je chybou toho clanku a jestli ne a ma to tak byt, tak tedy proc? Diky!

Matematické Fórum

#1 11. 01. 2018 16:11 — Editoval Zvedavec 4 (11. 01. 2018 23:50)

Chyba na Wiki ????

#2 12. 01. 2018 17:12 — Editoval Zvedavec 4 (12. 01. 2018 17:26)

Re: Chyba na Wiki ????

Zápatí