Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 02. 2018 10:35
- Vecerrov

- Příspěvky: 26
Rovnice s neznámou pod odmocninou
Dobrý den,
potřebovala bych pomoct s níže uvedeným příkladem. Výsledek má být 5 a když ho dosadím tak mi to vychází, ale nemůžu přijít na postup. Nejdřív mi vycházelo číslo 11, teď jak nad tím příkladem přemýšlím dál tak mi vychází pořád nějaké desetinné čísla.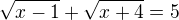
Offline
#2 04. 02. 2018 10:56
Re: Rovnice s neznámou pod odmocninou
↑ Vecerrov:
Zkus si to převést na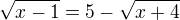
a umocnit celou rovnici, pak to budeš umocnit ještě jednou, kvůli tomu, že ti vznikne odmocnina po umocnění podle vzorce 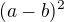
Offline
#3 04. 02. 2018 10:59
Re: Rovnice s neznámou pod odmocninou
↑ Vecerrov: Klasicky postup - obe strany umocnit na druhu.
Offline
#5 04. 02. 2018 13:29 — Editoval Jj (04. 02. 2018 13:32)
Re: Rovnice s neznámou pod odmocninou
↑ Kubas126:
Pozor, od druhého řádku není výpočet správně (chyba ve druhém řádku se projevuje v celém dalším výpočtu).
Pokud se tedy nemýlím.
Offline
#8 04. 02. 2018 13:39 — Editoval vlado_bb (04. 02. 2018 13:39)
#9 04. 02. 2018 13:39
Offline
#11 04. 02. 2018 14:12 — Editoval misaH (04. 02. 2018 14:12)
- misaH
- Příspěvky: 13459
Re: Rovnice s neznámou pod odmocninou
↑ Kubas126:
Nepozornosť?
Keby tebe ľudia takto radili...
Mal by si to radšej dať do Hide alebo v edite opraviť....
Offline
#13 04. 02. 2018 14:36
- misaH
- Příspěvky: 13459
Re: Rovnice s neznámou pod odmocninou
↑ Kubas126:
Umocniť, upraviť, vydeliť, umocniť.
A pozor na "vzorec" - znova tam bude.
Offline

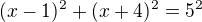
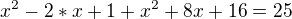
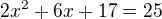
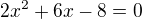
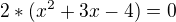
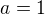
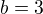
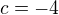
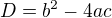
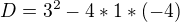
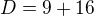
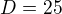
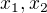 rovnice
rovnice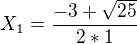
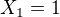
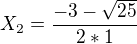
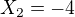
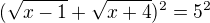
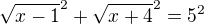
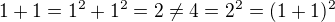 .
.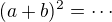

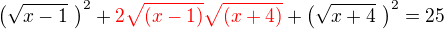
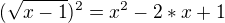 ?
? ?
?