Matematické Fórum

↑ AterCZ: Ahoj, neexistuje nic ako derivovanie cisel. Derivaciu maju funkcie. Je pravda, ze derivaciou konstantnej funkcie je nulova funkcia, ale funkcia nie je konstantna.

Rad poradim aj dalej, ak mas dalsie otazky, ale najprv prosim napis, z akej knihy studujes. Ak iba z poznamok alebo nahodne najdenych veci na internete, diskusia nebude mat zmysel.

↑ AterCZ:

Ahoj.

V pokročilejších partiích matematiky učit se z příkladů již nestačí, neboť
vzájemné souvislosti mezi pojmy zde již nebývají patrné na první pohled,
jak tomu bylo v matematických partiích nižšího stupně pokročilosti.
Především je potřeba znát obecnou teorii, abychom s její pomocí mohli
úlohu správně uchopit.

↑ AterCZ: Urcite by sa zislo pozriet si napriklad V. Jarnik: Diferencialni pocet 1

↑ AterCZ: Par uloh, na ktorych si mozes overit, ci spravne chapes pojem derivacia funkcie:

1. Nech . Aka je derivacia tejto funkcie?

2. 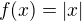nema derivaciu v nule.

3. Najdite priklad funkcie, ktora je definovana v kazdom 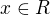, ale derivaciu ma iba v jednom bode.

↑ misaH: To je mi jasne, ved som aj pisal o pochopeni pojmu derivacia, nie o jeho rutinnom pouzivani. Na strednych skolach sa zejme uci (ak vobec) pouzivanie derivacie v istej triede funkcii, co je nieco ine ako pochopenie pojmu.

vlado_bb napsal(a):

↑ AterCZ: Par uloh, na ktorych si mozes overit, ci spravne chapes pojem derivacia funkcie:

1. Nech . Aka je derivacia tejto funkcie?

2. nema derivaciu v nule.

3. Najdite priklad funkcie, ktora je definovana v kazdom , ale derivaciu ma iba v jednom bode.

Ahoj, mohol by som sa spýtať na nejakú nápovedu k otázke 3)? Cítim že to bude nejaký trik, napr. keby nebola spojitá ale definovaná na celom R okrem nejakého bodu... hmm...

↑ vlado_bb:a to je práve ona funkcia nad ktorou uvažujem ale nenapadá ma... nejaká nápoveda?...

vlado_bb napsal(a):

↑ Peter_CSR: Skus nejakym sikovnym sposobom upravit Dirichletovu funkciu.

$f=\begin{cases}

oh, neviem to zapísať v latexe, takže:

D(x) je:

1, ak je x iracionálne
0, ak je x racionálne
1, ak je x 1

a derivácia je evidentne v 1.

Nebudem písať pre čo, ak je to správne nech sa potrápi aj OP, moja otázka len je: áno alebo nie?

↑ vlado_bb:

...aha tak... na toto nemám jednoducho matematický aparát... Ale celkom by ma zaújmalo riešenie, ak sa tu niekedy objaví...

↑ Peter_CSR:

Dirichletova funkce je obvykle definována předpisem

    D(x)  :=  1 ,  pokud   x   je racionální číslo,

    D(x)  :=  0 ,  pokud   x   je iracionální číslo, 

tedy opačně, než jak píšeš v ↑ Peter_CSR:.

(Stručněji lze říci, že D je  charakteristickou funkcí množiny všech racionálních čísel.)

Geometrický popis: Bod [t, D(t)]  leží na ose x, pokud t je iracionální, resp. na přímce
o rovnici  y = 1,  pokud  x je racionální (při obvyklém označení souřadnicových os,
pochopitelně).

Uvažovaná funkce D je v každém bodě svého definičního oboru nespojitá (zprava i zleva),
protože v každém bodě osy x platí, že libovolné jeho okolí (oboustranné či jednostranné)
obsahuje jak čísla racionální, tak i čísla iracionální. (V zájmu procvičení si proveď tento
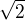důkaz podrobně - vyjdi z definice spojitosti a z faktů, že je racionální a iracionální).

Platí i další tvrzení:  Funkce D nemá v žádném bodě svého def. oboru derivaci zprava
ani zleva, vlastní ani nevlastní. (Opět si proveď podrobné důkazy - nejvíc se naučíš právě
pečlivým "sestrojováním" důkazů.)

Až tyto kroky zvládneš, zamysli se nad chováním funkcí

            ,     

v okolí bodu 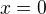 , tj. co můžeme říci o jejich spojitosti či derivaci v tomto bodě.

↑ Peter_CSR: O aku literaturu ide?