Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 02. 2018 15:31 — Editoval BobMarley (22. 02. 2018 15:35)
Derivace konstanty
Zdravím,
chtěl bych se zeptat, zda při dokazování derivace konstanty vzniká v poslední části důkazu neurčitý výraz  :
: ,
,
nebo nikoli:
Je mi jasné, že pro  je limita
je limita  , plyne to i ze smyslu derivace jako směrnice tečny, kdy je sklon (strmost, rychlost změny) konstantní funkce nulový.
, plyne to i ze smyslu derivace jako směrnice tečny, kdy je sklon (strmost, rychlost změny) konstantní funkce nulový.
Offline
#2 22. 02. 2018 16:07 — Editoval Rumburak (26. 02. 2018 13:28)
Re: Derivace konstanty
↑ BobMarley:
Ahoj. Žádný neurčitý výraz tam nevzniká (EDIT: postupujeme-li správně). Správný výpočet je ,
,
tj. úloha je převedena na limitu z konstatní funkce, speciálně z funkce konstatně rovné nule.
Offline
#3 22. 02. 2018 20:18
Re: Derivace konstanty
↑ Rumburak:
díky za odpověď.
První krok po zadání limity je dosazení do limity, pokud se čitatel limitně blíží 0, a současně jmenovatel blíží 0, pak se jedná o neurčitý výraz. Neodpovídá to tedy tomuto případu?
Offline
#4 22. 02. 2018 22:10
Re: Derivace konstanty
↑ kajbl:
Jenže čitatel se neblíží k nule, čitatel je nula (i když jmenovatel nula nebude, bude jen "blízký nule"). Takže pro všechna x, v okolí x0 bude výsledek přesně nula.
Já teda nevím přesně, co se myslí tím "neurčitým výrazem", vždycky jsem se s tím setkal v situaci, kdy ani čitatel, ani jmenovatel nebyly rovné nule v okolí toho bodu, kde počítáme limitu. Jestli se za neurčitý výraz považuje i 0/f(x) je asi věcí dohody.
Což mě ovšem přivádí na myšlenku, jaká by byla (a jestli ji vůbec lze určit) limita výrazu
Offline
#5 22. 02. 2018 22:26 — Editoval BobMarley (22. 02. 2018 23:25)
Re: Derivace konstanty
↑ MichalAld:
Ano, myslím, že s vámi souhlasím. O neurčitý výraz se podle mě také jednat nebude, protože čitatel je identicky roven nule a jmenovatel se neomezeně blíží nule. Proto budeme ve výpočtu pokračovat přesně tak, jak píše Rumburak.
Kdyby se podle mě jednalo o věc dohody a opravdu bychom uvažovali, že se jedná o neurčitý výraz, pak bychom danou limitu nedokázali určit (?), protože kdybych použili L´Hospitalovo pravidlo, pak by se jednalo o definici kruhem.
Co se týče Vaší limity, tak si myslím, že limita nelze určit, protože v tomto případě nenarážíme na neurčitý výraz v limitním smyslu ale na nedefinovaný výraz v algebraickém smyslu -> 0/0 = NAN.
Offline
#6 23. 02. 2018 08:15
Re: Derivace konstanty
↑ BobMarley: Staci sa pozriet na definiciu limity a uvedomit si, ze sa v nej hovori o PRSTENCOVOM okoli prislusneho bodu. Teda ziadne neurcite vyrazy, ziadne "blizenie sa k nule". Ide o podiel nuly a nenuloveho cisla, nic viac.
↑ MichalAld: Nejde o algebraicky vyraz, ale o akysi obrazok :) Rovnako dobre by sme sa mohli pytat na  a za tym obrazok nosorozca.
a za tym obrazok nosorozca.
Offline
#7 23. 02. 2018 19:10
Re: Derivace konstanty
vlado_bb napsal(a):
↑ MichalAld: Nejde o algebraicky vyraz, ale o akysi obrazok :) Rovnako dobre by sme sa mohli pytat na
a za tym obrazok nosorozca.
Já to nerozporuji, ale jak se to (tak na první pohled) pozná, že to není výraz, ale něco jako nosorožec?
Offline
#8 23. 02. 2018 19:26
Re: Derivace konstanty
↑ MichalAld: V tomto pripade podla nuly v menovateli. Vyraz 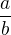 predstavuje realne cislo iba pre
predstavuje realne cislo iba pre 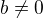 .
.
Offline
#11 24. 02. 2018 07:07 — Editoval vlado_bb (24. 02. 2018 07:08)
Re: Derivace konstanty
↑ BobMarley: Ak chceme uvazovat o  , tak
, tak  musi byt zobrazenie a
musi byt zobrazenie a  hromadny bod jeho definicneho oboru. Ak aj nazveme obrazok
hromadny bod jeho definicneho oboru. Ak aj nazveme obrazok  nejakym vznesenym nazvom (napriklad neurcity vyraz), zobrazenie s hromadnym bodom definicneho oboru
nejakym vznesenym nazvom (napriklad neurcity vyraz), zobrazenie s hromadnym bodom definicneho oboru  tym z neho neurobime.
tym z neho neurobime.
Offline
#12 24. 02. 2018 08:40
Re: Derivace konstanty
↑ vlado_bb: Jdi laskavě někam s těma "obrázkama" a používej zavedenou matematickou terminologii, tj. "neurčitý výraz".
Offline
#14 24. 02. 2018 09:16 — Editoval BobMarley (24. 02. 2018 09:16)
Re: Derivace konstanty
↑ Stýv:,↑ vlado_bb:
bavíme se o derivaci konstanty nebo o limitě MichalAld, tj  ?
?
V tom druhém se podle mě nemůžeme bavit o limitě funkce, protože se vůbec o funkci nejedná (tj. souhlasil bych s vlado_bb, jen bych výraz nenazýval neurčitý ale nedefinovaný).
Offline
#15 24. 02. 2018 11:53
Re: Derivace konstanty
↑ BobMarley: Přesně tak, nejedná se o funkci, ale o neurčitý výraz. Viz např. http://www.ucebnice.krynicky.cz/Matemat … vyrazy.pdf
Offline
#16 24. 02. 2018 12:05 — Editoval BobMarley (24. 02. 2018 12:54)
Re: Derivace konstanty
↑ Stýv:
Moc se mi nelíbí v tomto případě termín neurčitý výraz . Protože čitatel je identicky roven nule, stejně tak jmenovatel.
Takže daný výraz není algebraicky definovaný. Proto bych spíše opravdu volil termín nedefinovaný.
Protože o neurčitý výraz se jedná v případě, že  , tj. čitatel a jmenovatell se pouze blíží hodnotě 0.
, tj. čitatel a jmenovatell se pouze blíží hodnotě 0.
Na druhou stranu: danou limitu můžeme chápat jako podíl dvou konstantních funkcí (třebaže nulových). Potom bych se zase přikláněl k termínu neurčitý výraz.
Viz má otázka na začátku.
v tomto případě mě nenapadá, jak limitu vypočítat. Můžeme ji určit pouze pomocí úvahy viz vlado_bb
vlado_bb napsal(a):
↑ BobMarley: Staci sa pozriet na definiciu limity a uvedomit si, ze sa v nej hovori o PRSTENCOVOM okoli prislusneho bodu. Teda ziadne neurcite vyrazy, ziadne "blizenie sa k nule". Ide o podiel nuly a nenuloveho cisla, nic viac.
Offline
#17 24. 02. 2018 16:41 — Editoval Rumburak (24. 02. 2018 16:48)
Re: Derivace konstanty
↑ BobMarley:
Moje představa o tom, co je v teorii limit neurčitým výrazem, je následujíci:
Když k výpočtu limity tvaru např.
 , kde
, kde  jsou vhodné funkce,
jsou vhodné funkce,
nestačí znát limity  ,
,  (a "dosadit" je
(a "dosadit" je
do funkce  ).
).
Offline
#18 24. 02. 2018 17:47 — Editoval Marian (24. 02. 2018 17:48)
Re: Derivace konstanty
↑ Rumburak:
Nevím, zda je šťastné pokoušet se definovat něco jako "neurčitý výraz". Připadá mi to velmi subjektivní. Zkus například pozorovat funkce F(x,y)=sqrt(x-y), f(x)=x^4, g(x)=x^2 (snad se dají tyto funkce považovat za vhodné) a polož a=0.
Offline
#19 24. 02. 2018 20:29 — Editoval BobMarley (24. 02. 2018 20:32)
Re: Derivace konstanty
↑ Rumburak:
Máte pravdu, našel jsem na anglické wikipedii definici od Moigna, který říká něco v tomto smyslu:
Pokud po dosazení do předpisu limity vznikne výraz, pak tento výraz je neurčitý, jestliže neposkytuje dostatek informací k určení limity.
A v případě derivace konstanty, dostatek informací k určení limity máme. Proto se nejedná o neurčitý výraz.
Souhlasíte?
Offline
#20 25. 02. 2018 14:19
Re: Derivace konstanty
BobMarley napsal(a):
↑ Rumburak:
Máte pravdu, našel jsem na anglické wikipedii definici od Moigna, který říká něco v tomto smyslu:
Pokud po dosazení do předpisu limity vznikne výraz, pak tento výraz je neurčitý, jestliže neposkytuje dostatek informací k určení limity.
A v případě derivace konstanty, dostatek informací k určení limity máme. Proto se nejedná o neurčitý výraz.
Souhlasíte?
Už dlouho jsem horší radu pro výpočet limit nečetl (samozřejmě za to neodsuzuji tebe). To poukazuje především na fakt, že informace na Wikipedii je nutno brát se značnou rezervou.
Offline
#22 25. 02. 2018 14:47
Re: Derivace konstanty
↑ BobMarley:
Pokud to říkají vyučující vysokých škol, není to lichotivé zjištění. Výše Rumburakovi dávám jistý velmi snadný případ. Tedy ještě jednou.
Vypočti limitu
Offline
#23 25. 02. 2018 15:48 — Editoval BobMarley (25. 02. 2018 21:39)
Re: Derivace konstanty
↑ Marian:
Ještě k neurčitým výrazům, zde například Wolfram uvádí definici takto:
http://mathworld.wolfram.com/Indeterminate.html
Pokud jsem si ji dobře vyložil, tak říká něco podobného.
K Vaší limitě:
Po dosazení vyjde 0 (limita komplexní funkce).
Oním dosazením do limity funkce, vlastně říkáme, že funkce je na okolí bodu spojitá, a proto je limita funkce v bodě rovna funkční hodnotě.
Ovšem tato uvažovaná reálná funkce není na okolí bodu spojitá, a proto nemůžeme větu o limitě spojité funkce využít. A protože funkce není na okolí bodu 0 vůbec definována, pak v tomto bodě nemá limitu (plyne z epsilon-delta definice).
Offline
#24 26. 02. 2018 10:37 — Editoval Rumburak (26. 02. 2018 13:23)
Re: Derivace konstanty
↑ Marian:
Ahoj.
Onen svůj příspěvek jsem nemyslel jako definici nějakého pojmu, ale pouze jako koncept
příkladu, který si případný zájemce sám zkonkretisuje.
Pojem "neurčitý výraz" jsem sám od sebe, myslím, nikdy nepoužil a pokud jsem se s ním
někdy setkal, tak jsem ho vždy zařazoval pouze do metajazyka a tam by snad nemusel
nikomu vadit.
EDIT.
Funkce, z nichž je složena ta z příkladu 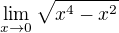 , nepovažuji z pohledu onoho
, nepovažuji z pohledu onoho
mého příspěvku za "vhodné", protože dotyčná složená funkce NENÍ definována na žádném
prstencovém okolí nuly, tudíž tato limita existovat nemůže již dle základního předpokladu
v definici limity.
Naproti tomu funkce  na nějakém prstencovém okolí nuly definována JE,
na nějakém prstencovém okolí nuly definována JE,
takže pokud by ani
(1) 
neexistovala, muselo by tomu tak být z jemnějších příčin než v případě předchozím. Někdo
by se možná při výpočtu kimity (1) pokusil využít úpravu tvaru
(2)  ,
,
tedy
 ,
,
kde ovšem na pravé straně formálně dostáváme 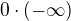 , což není korektní
, což není korektní
matamatický výraz, alespoň pokud chceme zůstat v oblasti klasické matematické analýzy.
To znamená, že i když dotyčná limita (1) existuje (což lze zjistit jiným způsobem),
postupem (2) ji určit nelze, neboť tento postup zde vedek k nedefinovanému neboli
neurčitému výrazu. Řekl bych, že toto pojmenování (v rámci metajazyka) je dáno jakousi
tradicí, která mne osobně nijak nepohoršuje. Ale připouštím, že to někdo může vidět jinak.
Offline
#25 26. 02. 2018 12:34 — Editoval Rumburak (26. 02. 2018 12:35)
Re: Derivace konstanty
↑ BobMarley:
Po zvážení bych to řekl takto:
Při výpočtu derivace konstanty se k neurčitému výrazu nemusíme dostat, pokud se
nedopustíme hrubé neobratnosti.
Offline
