Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 02. 2018 23:55
- jakubkoval

- Zelenáč
- Příspěvky: 24
- Škola: ZSGMIK
- Pozice: student
- Reputace: 0
Pravdepodobnosť - kocky
Zdravím, narazil som na problém pri príprave na test z matematiky.
Zadanie znie takto :
Hádžeme štyrmi kockami. Aká je pravdepodobnosť, že padne práve jedno z čísel 1,2,3?
Nikde na internete sa mi nepodarilo nájsť postup, ani návod ako podobný príklad riešiť, jediné čo som našiel je výsledok - 0,25.
Bude mi stačiť, ak ma niekto navedie, akým smerom mám ísť, ďakujem !
Offline
- (téma jako nevyřešené označil(a) gadgetka)
#2 27. 02. 2018 00:08
Re: Pravdepodobnosť - kocky
Ahoj, pokud budeme pocitat i s poradim kostek, tak pocet vsech moznych kombinaci je 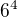 , na tos urcite prisel. Kolik je tech priznivych? Tak dejme tomu, ze na prvni kostce padlo neco z {1,2,3}, na zbylych kostkach pak muselo padnout cokoli z {4,5,6}. Kolik je to celkem moznosti? Protoze jsme uvazovali priznivou moznost na prvni kostce, musime jeste vysledny pocet moznosti vynasobit ctyrmi ;-)
, na tos urcite prisel. Kolik je tech priznivych? Tak dejme tomu, ze na prvni kostce padlo neco z {1,2,3}, na zbylych kostkach pak muselo padnout cokoli z {4,5,6}. Kolik je to celkem moznosti? Protoze jsme uvazovali priznivou moznost na prvni kostce, musime jeste vysledny pocet moznosti vynasobit ctyrmi ;-)
Offline
#3 27. 02. 2018 00:18
- jakubkoval

- Zelenáč
- Příspěvky: 24
- Škola: ZSGMIK
- Pozice: student
- Reputace: 0
Re: Pravdepodobnosť - kocky
↑ laszky:
jasné, po 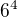 som došiel,
som došiel,
uvažoval som približne takto
priaznivé sú síce {1,2,3}, ale padnúť mi z nich môže iba jedno číslo, to znamená 1/6,
pre ostatné tri kocky mi teda ostáva {4,5,6} teda 3/6*3/6*3/6
v konečnom dôsledku teda 1/6*3/6*3/6*3/6
Teraz už však rozumiem, že z čísel 1,2,3 je mi jedno, ktoré vyberiem, teda nepočítam s 1/6, ale s 3/6
teda dostávam 3/6*3/6*3/6*3/6
a celé to musím prenásobiť štyroma, pretože mám 4 kocky, na ktorých sa to priaznivé môže stať.
takže finálny výpočet vyzerá asi takto
3/6*3/6*3/6*3/6*4 (=0,25)
Verím, že som to pochopil správne a veľmi pekne ďakujem za Váš čas!
Offline
#4 27. 02. 2018 00:20 — Editoval laszky (27. 02. 2018 00:21)
#5 27. 02. 2018 09:38
Re: Pravdepodobnosť - kocky
Zdravím všechny odborníky na pravděpodobnost. Myslím si, že řešení není správné, mohli byste mi to prosím buď potvrdit nebo vyvrátit? Děkuji. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#6 27. 02. 2018 13:10
Re: Pravdepodobnosť - kocky
↑ gadgetka:
Taky zdravím.
Možná něco přehlížím (nejsem tedy zrovna odborník), ale problém nevidím. V čem by mohl spočívat?
Pokud se tedy nemýlím.
Offline
#7 27. 02. 2018 15:01
Re: Pravdepodobnosť - kocky
Ahoj, snažím se to pochopit, protože příklady tohoto typu nejsou zrovna mojí silnou stránkou, nechápu a vrtalo mi hlavou, proč součiny už čtyř pravděpodobností ještě násobit čtyřmi, ale mám pocit, že mi právě svitlo, protože každá ta pravděpodobnost může být na libovolné kostce z těch čtyř, že? A ještě přemýšlím nad tím, když pravděpodobnost toho, že na jedné kostce padne např. 1, je 1/6, tak pravděpodobnost toho, co padne na ostatních kostkách je 5/6, ne?. Tak proč součin jedné z možností není 1/6 * 5/6 * 5/6 * 5/6 ... (ten bych pak násobila třemi, když je výběr z čísel 1, 2, 3 a to všechno tedy ještě čtyřmi). Nějak v tom vidím logiku víc než v tom, co je zde napsáno... :D
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#9 27. 02. 2018 16:01 — Editoval Jj (27. 02. 2018 16:03)
Re: Pravdepodobnosť - kocky
gadgetka napsal(a):
když pravděpodobnost toho, že na jedné kostce padne např. 1, je 1/6, tak pravděpodobnost toho, co padne na ostatních kostkách je 5/6, ne?
Hody jednotlivými kostkami jsou nezávislé - nezávislé jsou i pravděpodobnosti výsledků hodů. Zřejmě by se spíše mělo říci
když pravděpodobnost toho, že na jedné kostce padne v jednom hodu např. 1, je 1/6, tak pravděpodobnost toho, že na jedné kostce v jednom hodu nepadne 1, je 5/6
A teď jde o to, co nás v úloze zajímá:
Jev A: V jednom hodu jednou kostkou padne právě jedno z čísel 1, 2, 3,
P(A) = p = 3/6 = 1/2
Jev B: V jednom hodu jednou kostkou nepadne žádné z čísel 1, 2, 3.
P(B) = q = 1-P(A) = 1/2
Pak pravděpodobnost hledaná v úloze bude
Edit - pozdě, ale nechám (když už jsem to tak dlouho klupal)
Pokud se tedy nemýlím.
Offline
#10 27. 02. 2018 16:54 — Editoval Rumburak (28. 02. 2018 12:50)
Re: Pravdepodobnosť - kocky
Hádžeme štyrmi kockami. Aká je pravdepodobnosť, že padne práve jedno z čísel 1,2,3?
Ahoj.
Moje řešení: EDIT : AVŠAK JINÉ ÚLOHY - viz potnámka v závěru.
Zkusme vyjít z klasické definice pravděpodobnosti.
Podmínka definující náš jev při hodu 4-mi kostkami znamená, že
1. Ze čtveřice kostek má být vybrána trojice (A, B, C) , což je možno provést
volbou kostky D, tedy 4-mi způsoby.
2. Na koskách A, B, C mají padnout celkem všechna číísla 1, 2, 3 (což v tomto případě
znamená totéž jako "každé právě jednou").
Počet těchto možností je roven počtu permutací 3-prvkové množiny, což je 3!
(vykřičníkem je míněn operátor faktoriálu).
3. na kostce D má padnout padnout některé z číel 4, 5, 6, což jsou 3 možnosti.
Celkem máme 4 * 3! * 3 možností, jak naplnit daný jev.
Počet všech možností, jak může dopadnout hod 4-mi kostkami, pokud mezi nimi
rozlišujeme (prozatím jsme tak činili), je 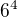 .
.
EDIT. V předchozím výpočtu jsem omylem pracoval s jiným zadáním. Podmínku
"padne práve jedno z čísel 1,2,3"
jsem zaměnil za podmínku "každé z čísel 1, 2, 3 padne právě jednou".
Omlouvám se.
Offline
#11 28. 02. 2018 11:08
- jakubkoval

- Zelenáč
- Příspěvky: 24
- Škola: ZSGMIK
- Pozice: student
- Reputace: 0
Re: Pravdepodobnosť - kocky
↑ Rumburak:
Zdravím,
"Na koskách A, B, C mají padnout celkem všechna číísla 1, 2, 3 (což v tomto případě
znamená totéž jako "každé právě jednou"). "
Zo zadania to takto nechápem, skôr to chápem ako
hádžeme 4 kocky, aká je pravdepodobnosť, že medzi 4 padnutými číslami bude práve raz jedno číslo z množiny {1,2,3}
(to znamená, že keď už raz padne 1 (resp. 2, resp. 3) tak už na dalších kockách nemôže padnúť nič z množiny {1,2,3}
Opravte ma ak sa mýlim.
Z vášho výpočtu chápem, že v závere delím 4*3!*3/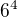 , to mi však nedáva správny výsledok.
, to mi však nedáva správny výsledok.
Ďakujem za váš čas! :)
Offline
#12 28. 02. 2018 11:11
- jakubkoval

- Zelenáč
- Příspěvky: 24
- Škola: ZSGMIK
- Pozice: student
- Reputace: 0
Re: Pravdepodobnosť - kocky
↑ Jj:
Wau, tak toto riešenie mi pomohlo ešte viac pochopiť princíp kociek!
Veľmi Vám ďakujem, za tento výpočet, postup a vysvetlenie!
P.S. - nikdy nie je "pozdě" :D
Offline
#13 28. 02. 2018 11:39
Re: Pravdepodobnosť - kocky
↑ jakubkoval:
Omlouvám se - nejspíš jsem si špatně přečetl zadání. Podmínku, že padne práve jedno
z čísel 1,2,3, jsem zaměnil za podmínku "každé z čísel 1, 2, 3 padne právě jednou".
Offline

