Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 03. 2018 21:40
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Záměna sumy
Ahoj,
žádám o radu, nejlépe o odkaz, kde si můžu přečíst důkaz k této záměně sum.
Děkuji
P.K.
Offline
- (téma jako nevyřešené označil(a) PlusPlusPlus)
#2 08. 03. 2018 22:06
Re: Záměna sumy
↑ PlusPlusPlus: Ide o sucet horneho trojuholnika stvorcovej matice, raz po riadkoch a raz po stlpcoch. Dokaz je zalozeny na komutativnosti scitania.
Offline
#4 09. 03. 2018 17:47 — Editoval PlusPlusPlus (09. 03. 2018 17:48)
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Záměna sumy
Zdravím,
děkuji za odpovědi. Jestli to dobře chápu, tak jde vlastně o dvojný integrál. V tomto případě je uzavřená oblast integrování tento pravoúhlý trojůhelník. Jednou je to integrované v pořadí djdk, podruhé dkdj.
V jiném případě, např.  , kdy jsou dvě sumy za sebou a kdy sčítání nezávisí ani na jedné proměnné, tak je integrovanou oblastí takového dvojného integrálu obdelník, nebo čtverec. Proto můžu přehazovat pořadí sumy dle libosti.
, kdy jsou dvě sumy za sebou a kdy sčítání nezávisí ani na jedné proměnné, tak je integrovanou oblastí takového dvojného integrálu obdelník, nebo čtverec. Proto můžu přehazovat pořadí sumy dle libosti.
Pro obecnou uzavřenou oblast u dvojné sumace však neplatí totéž co pro dvojný integrál. Proto nemůže platit u sumace obecná Fubiniova věta, pouze ta diskrétní.
Když tak nad tím přemýšlím, tak mě nenapadá další uzavřená oblast , kde by se u dvojných sumací dala využít taková pěkná identita jako již zmiňované identity pro oblasti čtverce a trojuhelníka.
Snad jsem to tedy pochopil a děkuji za Váš čas a odpovědi.
Offline
#5 10. 03. 2018 05:26 — Editoval Marian (10. 03. 2018 07:23)
Re: Záměna sumy
Vážení, téma je sice již označeno jako vyřešené, ale zdá se mi, že některé skutečnosti mohly zaznít a nestalo se tak.
1. (↑ vlado_bb:) Nějak nevidím, jak by se přímo měla používat komutativita sčítání. Jmenovaná vlastnost této operace je jedním ze základních praktických požadavků na ni. K důkazu jsem ji (přímo) nepotřeboval, viz bod 3. níže.
2. (↑ laszky:) Správný postřech o diskrétní analogii s vlastností dvojného integrálu je hezký. Ovšem v případě práce se sumou (natož konečnou a takto snadnou) mi to připadá jako mírně nadbytečné, a to především v souvislosti: (a) s první větou mého příspěvku a jeho textem v bodu 3. níže, (b) s původní otázkou tazatele.
3. Očekával bych, že někdo navrhne důkaz matematickou indukcí. Je tak směšně snadný a přímočarý, že ho přenechávám jako formu vtipu původnímu tazateli.
Offline
#6 10. 03. 2018 12:12 — Editoval vlado_bb (10. 03. 2018 12:13)
Re: Záměna sumy
↑ Marian: Este k tej komutativnosti. Rovnost v povodnom prispevku pre napriklad  je takato:
je takato: .
.
Podobne aj pre ine  ide o scitanie tej istej konecnej mnoziny realnych cisel raz v jednom, raz v inom poradi. Otazka znela, preco sa tieto sucty rovnaju. Myslim, ze poukazanie na komutativitu je pre pochopenie rovnosti podstatne. Samozrejme, suhlasim s tym, ze indukcia je zrejme najjednoduchsia metoda formalneho dokazu. Rovnako aj s tym, ze Fubiniho veta je uz asi za hranicou povodnej otazky, aj ked suvislost tu pochopitelne je.
ide o scitanie tej istej konecnej mnoziny realnych cisel raz v jednom, raz v inom poradi. Otazka znela, preco sa tieto sucty rovnaju. Myslim, ze poukazanie na komutativitu je pre pochopenie rovnosti podstatne. Samozrejme, suhlasim s tym, ze indukcia je zrejme najjednoduchsia metoda formalneho dokazu. Rovnako aj s tym, ze Fubiniho veta je uz asi za hranicou povodnej otazky, aj ked suvislost tu pochopitelne je.
Offline
#7 10. 03. 2018 19:50
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Záměna sumy
Ahoj,
1. ověřím pro 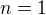
 implikuje
implikuje  , tedy rovnost platí
, tedy rovnost platí
2. Předpokládám tedy, že vztah platí i pro libovolné n 
3. Dokázuji že rovnost platí i pro n+1  upravím pravou stranu
upravím pravou stranu 
Do pravé strany rovnice dosadím indukční předpoklad 
a je hotovo 
Tak díky všem za příspěvky.
Offline
#8 10. 03. 2018 20:30 — Editoval PlusPlusPlus (10. 03. 2018 20:48)
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Záměna sumy
↑ Marian:
Ještě mě tak napadlo takovéto zobecnění
kde  jsou nějaká celá čísla, současně
jsou nějaká celá čísla, současně  je menší nebo rovno
je menší nebo rovno  . Tady indukce nezafunguje.
. Tady indukce nezafunguje.
Tady bys jak postupoval?
Offline
#9 24. 04. 2018 12:13
#10 24. 04. 2018 12:42
Re: Záměna sumy
↑ PlusPlusPlus: Aj tu ide iba o sucet tych istych cisel, raz v istom poradi, raz zasa v inom.
Offline
