Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#51 31. 01. 2017 11:35 — Editoval vanok (01. 02. 2017 06:36)
Re: Limitny maraton
Cvicenie 14.
Riesenie, prva cast.
Polozme 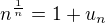 , kde
, kde  ( pochopitelne )
( pochopitelne )
Newton-ov binom sa pise
Vsetko cleny su kladne
Tak 
Co da  kde prava cast vyrazu ide k nule ked n rastie.
kde prava cast vyrazu ide k nule ked n rastie.
Dokoncenie....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#52 08. 02. 2017 05:23 — Editoval vanok (08. 02. 2017 12:53)
Re: Limitny maraton
Cvicenie 14
Druha cast riesenia a ukoncenie.
Tak pre kazde  , mame
, mame  pre dost velke n, cize
pre dost velke n, cize 
Nic nam nebrani vybrat  , a preto
, a preto  konverguje k 0.
konverguje k 0.
Teraz mozte ukoncit cvicenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#53 04. 03. 2018 19:07
Re: Limitny maraton
Navrat k cviceniu 13.
Zda sa, ze toto klasicke cvicenie je oblubene vela skusajucimi a malo studentov sa nad nim zamyslelo
Skoda, lebo je uzitocne ho vediet vyriesit.
Tak teraz, dam odpoved na obe otazky cvicenia, co dufam motivuje niekolko foristov.
Odpoved na prvu otazku je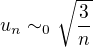
a na druhu 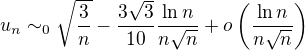
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#54 06. 03. 2018 08:52
Re: Limitny maraton
Cvicenie 13. Prva cast. (Podrobne riesenie)
Interval ![kopírovat do textarea $]0; \frac {\pi}2 ]$](/mathtex/9d/9dba2de83ed6b23d7bec75099fa28894.gif) je stabiny pre funkciu
je stabiny pre funkciu 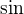 a preto
a preto ![kopírovat do textarea $u_n \in ]0; \frac {\pi}2 ]; \forall n$](/mathtex/6e/6e64307c8879e8c7599995c4112fdbe6.gif) .
.
A tiez  na tomto intervale.
na tomto intervale.
A tak postunnost 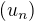 je ostro klesajuca.
je ostro klesajuca.
Na viac je minorovana cislom 0, a tak konverguje.
Pre jej limitu  plati
plati 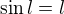 co da
co da 
Co sa tyka envivalentu  , poznamenajme, ze
, poznamenajme, ze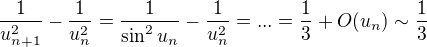
Tento ekvivalant na ukazuje, ze rad
 diverguje.
diverguje. A tak

Inac povedane
 ,
, a konecne
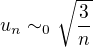 .
. Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#56 06. 03. 2018 09:59
Re: Limitny maraton
Pozdravujem ↑ Pavel:, pozri si PM.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#57 10. 03. 2018 23:50 — Editoval vanok (10. 03. 2018 23:57)
Re: Limitny maraton
Cvicenie 13.
Druha cast. [riesenie na doplnenie]
Aj tu hladajme najprv asymptoticky rozvoj 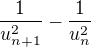 ( podobne ako v prvej casti).
( podobne ako v prvej casti).
Tu vsak podme o jeden clen dalej ako v predoslej casti:
Cize 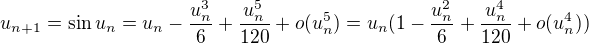
Co da 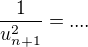 ( doplnte ...)
( doplnte ...)
Potom 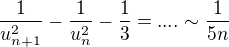 ( aj tu doplnte vypocty ......).
( aj tu doplnte vypocty ......).
[ Tu tiez ako v prvej casti, posledny vyraz je clen divergentnej rady a preto mozeme scitat ekvivalenty ]
Z toho 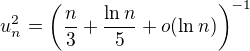
A nakoniec ukoncite vypocet a tak dostanete hladany rozvoj.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#58 11. 03. 2018 02:55 — Editoval vanok (11. 03. 2018 02:57)
Re: Limitny maraton
Cvicenie 13.
Addendum.
Vysetrenie 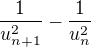 v prvej casti cvicenia sa moze zdat niektorym foristom priliz trikove.
v prvej casti cvicenia sa moze zdat niektorym foristom priliz trikove.
Tak tu pridam malu uvahu, ktora ich presveci, ze ide o nieco velmi prirodzene.
Polozme si takuto otazku:
Urcite realne cislo take, ze postupnost
take, ze postupnost 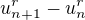 ma konecnu nenulovu realnu limitu.
ma konecnu nenulovu realnu limitu.
Dam tu hned cele riesenie, co moze byt aj kontrola pre tych, ktori doplnili casti z .... prvej casti cvicenia 13. 

A pre 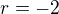 dostaneme
dostaneme 
Pochopitelne som mohol toto dat do textu cvicenia, ale ak niekto rozmyslal o tomto cviceni, iste na to prisiel aj sam. 😁
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#59 12. 03. 2018 22:29 — Editoval vanok (12. 03. 2018 22:29)
Re: Limitny maraton
Akoze, limitovane rozvoje su uzitocne na hladanie niektorych limit, tak vam tu pridavam
Cvicenie 15. (Aproximacia  ).
).
Najdite 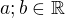 take aby
take aby 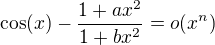 pre co najvädcie
pre co najvädcie  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#60 13. 03. 2018 00:44
Re: Limitny maraton
Cviceni 15.
Pouzijeme Taylorovu radu pro kosinus: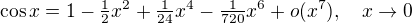 .
.
Nyni se pokusime tuto radu napodobit: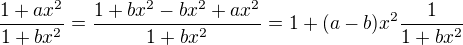 .
.
Vidime, ze musi platit  . Dale
. Dale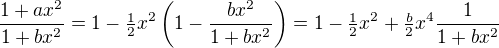 ,
,
a tedy 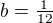 . Muzeme pokracovat analogicky a ziskat nakonec napr.
. Muzeme pokracovat analogicky a ziskat nakonec napr.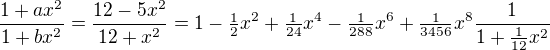 .
.
(Vidime, ze jsme mohli rovnou pouzit soucet geometricke rady.) Celkem tedy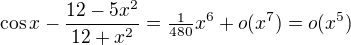 .
.
Offline
#61 13. 03. 2018 02:31 — Editoval vanok (13. 03. 2018 02:35)
Re: Limitny maraton
Pozdravujem ↑ Bati:,
Ano to je cakana odpoved.
( poznamka: ide o aproximaciu funkcie cos pre 0,1 priblizne 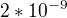 )
)
Mozes, prosim, dat vlastne cvicenie 16, ktore by mohlo byt polozene na skuskach.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#62 13. 03. 2018 11:06
Re: Limitny maraton
↑ vanok:
Otázku řeší tzv. Padého aproximace.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#63 13. 03. 2018 19:28
Re: Limitny maraton
Pozdravujem ↑ Pavel:,
Ano mas pravdu, cvicenie 15 moze byt povazovane ako jeden uvodny priklad z Padé approximation.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#64 13. 03. 2018 21:00 — Editoval Bati (13. 03. 2018 21:01)
Re: Limitny maraton
↑ Pavel:↑ vanok:
Zajimave je take srovnani s "globalni" aproximaci.
Cviceni 16.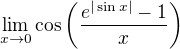
Offline
#65 15. 03. 2018 08:20
Re: Limitny maraton
Pozdravujem ↑ Bati:,
Aby ostalo toto vlakno zive, tak si dovolim reagovat.
Moje riesenie tejto limity spociva na limitovanom rozvoji 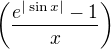 pre
pre  a pre
a pre  v okoli
v okoli  . ( rad 2 staci). A potom sa ukonci vdaka spojitosti funkcie
. ( rad 2 staci). A potom sa ukonci vdaka spojitosti funkcie 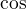 .
.
Ake je tvoje riesenie?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#68 16. 03. 2018 11:15
Re: Limitny maraton
Pozdravujem ↑ Pavel:,
Zaujimave cvicenie.
Male otazky.
V tvojom cviceni vyuzijes, ze 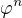 je pre dostatocne velke
je pre dostatocne velke  « skoro cele » cislo? A tiez vyuzijes, ze ide o « Pisot-ove » cislo?
« skoro cele » cislo? A tiez vyuzijes, ze ide o « Pisot-ove » cislo?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#70 23. 03. 2018 02:27 — Editoval vanok (24. 03. 2018 09:11)
Re: Limitny maraton
Ahoj ↑ Pavel:,
Este jedna mala pomoc.
K cviceniu 17 som zabudol pridat, ze je vyhodne vediet, ze 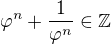 co sa lahko dokaze napr. indukciou.
co sa lahko dokaze napr. indukciou.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#71 23. 03. 2018 21:44 — Editoval vanok (24. 03. 2018 08:23)
Re: Limitny maraton
Pozdravujem ↑ Pavel:,
Aby sme neprerusili dynamiku tohto vlakna ( i ked na cvicenie 17 ziadny student nereagoval), ( Ak mozes napis tvoje riesenie tohto cvicenia, alebo aspon “hint” na tvojo riesenie, ak nejdes tou istou cestov ako som naznacil) a ja
hned pridavam cvicenie 18.
Urcite ci rad vseobecneho clenu 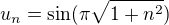 je alebo konvergentny, alebo divergentny.
je alebo konvergentny, alebo divergentny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#73 25. 03. 2018 06:20
Re: Limitny maraton
Coucou ↑ laszky:,
Zaujimave.
Hint na pokracovanie.
Dobry zaciatok. A tak ten rad konverguje? Ci nie?
Odpoved sa najde vdaka vysetreniu 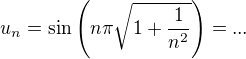
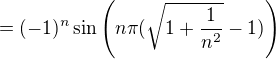
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#74 26. 03. 2018 05:01
Re: Limitny maraton
↑ vanok:
Pozdravujem. Mozna by to obcas chtelo pouzit symbol  ... Napr.
... Napr. 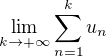 , nebo
, nebo  , pak by mi mozna doslo, co se pozaduje ;-)
, pak by mi mozna doslo, co se pozaduje ;-)
Jinak, protoze 
 ,
,
jde 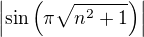 monotonne k nule a
monotonne k nule a 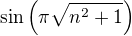 strida znamenka. Podle Leibnitzova kriteria tedy
strida znamenka. Podle Leibnitzova kriteria tedy 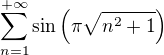 konverguje.
konverguje.
Offline
#75 26. 03. 2018 18:22
Re: Limitny maraton
Hallo ↑ laszky:,
Ide o cvicenia typu skuska. Vtedy je dolezite si dobre precitat text cvicenia a neriesit nieco ine ako polozene otazky.
Dakujem, ze si na to upozornil inych foristov.
Co sa tyka pouzivania 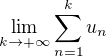 ,
,  tak je dobre vediet, ze takyto zapis ma byt pouzity len ak dana limita existuje. Inac by to mohlo oznacit limitu, ktora neexistuje. ... a tomu sa normalne treba vyhybat.
tak je dobre vediet, ze takyto zapis ma byt pouzity len ak dana limita existuje. Inac by to mohlo oznacit limitu, ktora neexistuje. ... a tomu sa normalne treba vyhybat.
Dalsie cvicenia pridu co nevidiet. Ak nie inym, tak tebe urobia radost. 🙂
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

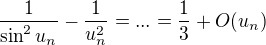

 je zlatý řez.
je zlatý řez.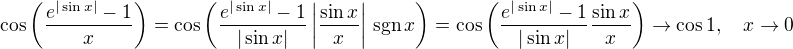 .
.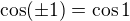 .
.
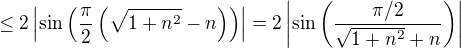 ,
,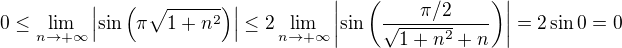 .
.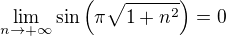 .
.