Matematické Fórum

↑ zswx: Ahoj,
stačí dať do rovnosti vzorec pre obvod a obsah kruhu.

↑ zswx:
obvod: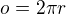
obsah:
Musí platiť: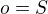
Čiže dosaď vzorce, vykráť a vyjadri .

To je ovšem pěkně hloupý příklad, protože po nás chce, abychom dali do rovnosti délku a plochu, což ve skutečném světě nemůžeme nikdy udělat, protože délka a plocha jsou v jiných jednotkách.

Takto (čistě matematicky) nám sice vyjde, že r=2, ale mohou to být dva palce, dva metry, dva světelné roky - a při troše fantazie zjistíme, že ten kruh může být úplně libovolně velký, protože vždy můžeme zvolit takovou jednotku délky, aby mám velikost (libovolného) kruhu vyšla 2. Protože jednotky délek si můžeme volit zcela libovolně.

↑ Blackflower:
Čistě matematicky je to samozřejmě v pořádku.
Jenže když budeme dělat "matematiku jen pro matematiku", nebude z ní žádný relálný úžitek. Užitek je z ní jen tehdy, když se její výsledky dají použít i v reálném (skutečném) světě.
A abychom to mohli dělat, je třeba přidat navíc pár požadavků, které jsou někdy tak samozřejmé, že se nad tím už nikdo ani nepozastavuje, takže to člověk vlastně ani nikde neuslyší.

Jedna z věcí je, že pokud chceme reálný svět popisovat čísly, musíme si také zvolit ty "základní jednotky". Nemá žádný smysl říct, že vzdálenost mezi Prahou a Brnem je 200 000. Jediné, co má smysl říct je že ona vzdálenost je 200000x větší než ta tyčka, co mám opřenou v koutě (a říkám jí "metr").

A musíme zajistit, aby vztahy, které mají popisovat náš skutečný svět nezávisely na tom, jak velké si ty základní jednotky zvolíme (jak dlouhou si tu "metrovou tyč" uříznu). Proto se taky ve všech fyzikálních zákonech objevují takové ty konstanty, které nám korigují naši volbu jednotek - podle toho, jak si zvolíme jednotky, takové máme konstanty.

A příklad s kruhem (o obvodu rovném obsahu) je zrovna příklad, který nemůže popisovat skutečný svět, nemůže popisovat žádný "skutečný, existující kruh". Protože všechny předpovědi stran skutečných kruhů nemohou záviset na tom, jaké si zvolíme základní jednotky.

Je to přesně příklad takové "matematiky jen pro matematiku", jenže na to studenty nikdo neupozorní.

Takto to vede na představu, že existují kruhy, které mají větší plochu než obvod, a kruhy které mají menší plochu než obvod, a to už jsme jen kousek od představy, že existují topné spirály, na kterých je napětí menší než výkon a topné spirály kde je napětí větší než výkon. A za chvíli se můžeme dostat k tomu, že velikost závaží je větší nebo menší než jeho hmotnost, a potažmo k tomu, že doba, než zmíněné závaží spadne ze stolu na zem je větší nebo menší než jeho hmotnost.


Pokud bychom sestrojili kruh, který má ve středu Prahu a někde na obvodu Brno a ptali se, zdali je jeho plocha větší než obvod, můžeme dostat dost rozdílné odpovědi. Pokud budeme měřit délky ve světelných letech, dostaneme odpověď že plocha kruhu je zcela zanedbatelná ve srovnání s jeho obvodem. Pokud budeme jako jednotku délky používat velikost vodíkového atomu, dostaneme odpověď, že plocha onoho kruhu je mnohem, mnohem větší, než jeho obvod.

Ale přitom je to pořád ten samý kruh, má pořád ten samý obvod a tu samou plochu.

Ve fyzice říkáme, že takovéto tvrzení (předpovědi, výsledky) které závisí na něčem, co si můžeme libovolně zvolit, nemohou mít fyzikální význam. Nemohou popisovat nic ze skutečného světa.

Jinak by to bylo super - mohli bychom si takto udělat definici metru - že je to taková délka, při které má kruh stejný obvod jako obsah. A žádný "skutečný etalon" odněkud z Paříže bychom vůbec nepotřebovali...